The convergence rate

We can now analyze which of the particular choices of $\gamma$ is more appropriate as far as the convergence rate is concerned.

If we consider the general form of the square root iteration

$$x_{n+1}=\frac{s+x_{n}\gamma}{x_n+\gamma}$$

we can estimate the convergence rate by the difference between the actual estimation at step (n+1) and the analytical value $\sqrt{s}$. For the general case, we obtain

$$x_{n+1}-\sqrt{s} = \frac{s+\gamma x_n -x_n \sqrt{s}-\gamma \sqrt{s}}{x_n+\gamma}$$

or  

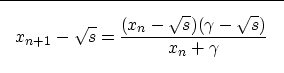$$\fbox {$ \displaystyle x_{n+1}-\sqrt{s} = \frac{(x_n-\sqrt{s})(\gamma-\sqrt{s})}{x_n+\gamma} $}$$ (7)

 

sqroot Figure 2 Convergence plots for different recursive algorithms, shown in Table 1.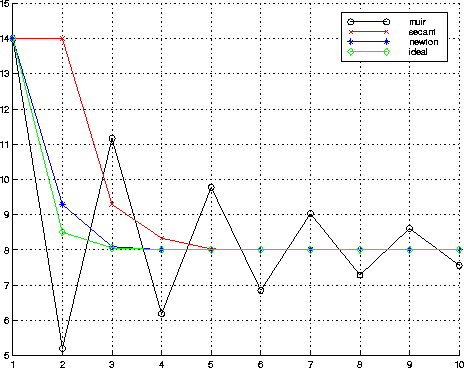

The possible selections for $\gamma$ from Table 1 clearly show that the recursions described in the preceding subsection generally have a linear convergence rate (that is, the error at step n+1 is proportional to the error at step n), but can converge quadratically for an appropriate selection of the parameter $\gamma$, as shown in Table 7. Furthermore, the convergence is faster when $\gamma$ is closer to $\sqrt{s}$.

   

$$\gamma$$ Convergence

Muir 1 linear

Secant x_n-1 quasi-quadratic

Newton x_n quadratic

We therefore conclude that Newton's iteration has the potential to achieve the fastest convergence rate. Ideally, however, we could use a fixed $\gamma$ which is a good approximation to the square root. The convergence would then be slightly faster than for the Newton-Raphson method, as shown in Figure 2.