




Next: A comparison with the
Up: Sava & Fomel: Spectral
Previous: The convergence rate
We can now extend the equations derived for real numbers to
polynomials of Z, with 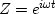 , and obtain spectral
factorization algorithms similar to the Wilson-Burg method
Sava et al. (1998), as follows:
, and obtain spectral
factorization algorithms similar to the Wilson-Burg method
Sava et al. (1998), as follows:
| 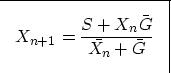 |
(8) |
If L represents the limit of the series in (8),
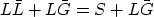
and so
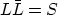
Therefore, L represents the causal or anticausal part of the given
spectrum 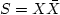 .
.
Table 3 summarizes the spectral factorization
relationships equivalent to those established for real numbers in
Table 1.
Table 3:
Spectral factorization
| General |
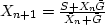 |
| Muir |
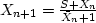 |
| Secant |
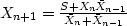 |
| Newton |
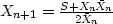 |
| Ideal |
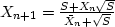 |
The convergence properties are similar to those derived for
real numbers. As shown above, the Newton-Raphson method should have
the fastest convergence.





Next: A comparison with the
Up: Sava & Fomel: Spectral
Previous: The convergence rate
Stanford Exploration Project
4/20/1999
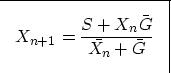
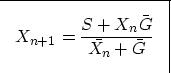
![]()
![]()
![]() .
.