![]()
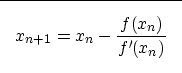 |
(1) |
A common choice of the function f is f(x)=x2-s. This function has the advantage that it is easily differentiable, with f'(x)=2x. The recursion relation thus becomes
![]()
![]()
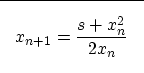 |
(2) |
The recursion (2) converges to ![]() depending
on the sign of the starting guess
depending
on the sign of the starting guess ![]() .
.
A variation of the Newton-Raphson method is to use a finite approximation of the derivative instead of the differential form. In this case, the approximate value of the derivative at step n is
![]()
For the same choice of the function f, f(x)=x2-s, we obtain
![]()
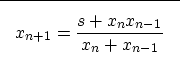 |
(3) |
In this case, recursion (3) also converges to ![]() depending on the sign of the starting guesses x0 and
x1.
depending on the sign of the starting guesses x0 and
x1.
Another possible iterative relation for the square root is Francis Muir's, described by Jon Claerbout 1995:
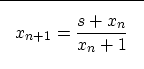 |
(4) |
This relation belongs to the same family of iterative schemes as Newton and Secant, if we make the following special choice of the function f(x) in (1):
| |
(5) |
Figure 1 is a graphical representation of the function f(x).
|
muf
Figure 1 The graph of the function defined in Equation (1) used to generate Muir's iteration for the square root (solid line). The dashed lines are the plot of the two factors in the equation . | 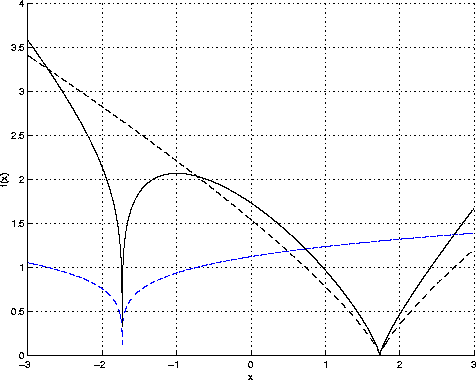 |
From the analysis of equations (2), (3), and (4), we can derive the following general form for the square root iteration:
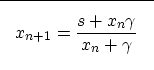 |
(6) |