




Next: Numerical examples
Up: VTI processing in inhomogeneous
Previous: raytracing equations
Following the approach of Alkhalifah (1997b), an acoustic wave equation is simply derived from the eikonal
equation using Fourier transformations.
The addition of  results in a more intriguing wave equation than the one derived by Alkhalifah.
Instead of the symmetric form of the familiar Laplacian in isotropic media,
two sources of unsymmetry are introduced into the new
wave equation. One is caused by the unbalanced new coordinate
system with one axis given in time and the other in position.
The second, caused by anisotropy, is similar to that which Alkhalifah described.
results in a more intriguing wave equation than the one derived by Alkhalifah.
Instead of the symmetric form of the familiar Laplacian in isotropic media,
two sources of unsymmetry are introduced into the new
wave equation. One is caused by the unbalanced new coordinate
system with one axis given in time and the other in position.
The second, caused by anisotropy, is similar to that which Alkhalifah described.
Using 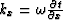 , and
, and
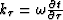 ,
where kx is the horizontal component of the wavenumber vector,
,
where kx is the horizontal component of the wavenumber vector, 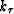 is the
vertical-time-normalized component
of the wavenumber vector, and
is the
vertical-time-normalized component
of the wavenumber vector, and
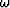 is the angular frequency, we can transform
equation (9) to
is the angular frequency, we can transform
equation (9) to
| 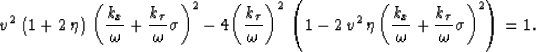 |
(22) |
Multiplying both sides of equation (22) with the wavefield in the Fourier domain, 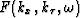 ,as well as using inverse Fourier transform on
,as well as using inverse Fourier transform on 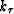 , kx
and
, kx
and 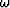 (
(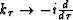 ,
, 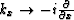 , and
, and
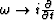 ), we obtain the acoustic wave equation in
this new vertical-velocity-independent coordinate system,
), we obtain the acoustic wave equation in
this new vertical-velocity-independent coordinate system,
| 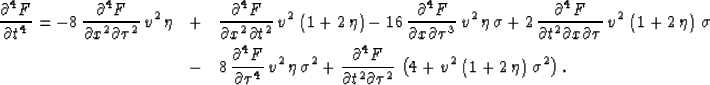 |
|
| (23) |
This equation is a fourth-order partial differential equation. Unlike, the acoustic wave equation for
VTI media
of Alkhalifah (1997b), equation (23) has odd-order derivatives caused by the unsymmetry of the
coordinate system. Setting 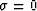 [v(z)=0], we obtain a similar equation, with
[v(z)=0], we obtain a similar equation, with 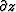 replaced by
replaced by 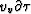 as follows:
as follows:
| 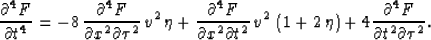 |
(24) |
Setting 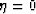 in equation (23) yields the acoustic equation for
elliptically anisotropic media:
in equation (23) yields the acoustic equation for
elliptically anisotropic media:
| 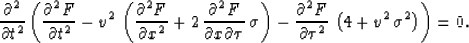 |
(25) |
Substituting 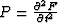 , we obtain the second-order
wave equation for elliptically
anisotropic media:
, we obtain the second-order
wave equation for elliptically
anisotropic media:
| 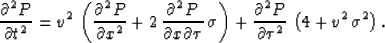 |
(26) |
Rewriting equation (23) in terms of P(x,y,z,t) rather than F(x,y,z,t),
wherever possible, yields
| 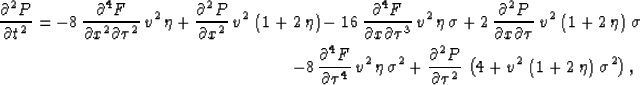 |
|
| (27) |
where
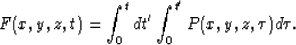
Because of its second-order nature in time, equation (27) is simpler
to use in a numerical implementation than
equation (23). The acoustic wave equation in  -domain is clearly
independent of the vertical velocity when
-domain is clearly
independent of the vertical velocity when  is given by equation 12 and
is given by equation 12 and
 is laterally invariant.
is laterally invariant.





Next: Numerical examples
Up: VTI processing in inhomogeneous
Previous: raytracing equations
Stanford Exploration Project
9/12/2000
![]() results in a more intriguing wave equation than the one derived by Alkhalifah.
Instead of the symmetric form of the familiar Laplacian in isotropic media,
two sources of unsymmetry are introduced into the new
wave equation. One is caused by the unbalanced new coordinate
system with one axis given in time and the other in position.
The second, caused by anisotropy, is similar to that which Alkhalifah described.
results in a more intriguing wave equation than the one derived by Alkhalifah.
Instead of the symmetric form of the familiar Laplacian in isotropic media,
two sources of unsymmetry are introduced into the new
wave equation. One is caused by the unbalanced new coordinate
system with one axis given in time and the other in position.
The second, caused by anisotropy, is similar to that which Alkhalifah described.
![]() , and
, and
![]() ,
where kx is the horizontal component of the wavenumber vector,
,
where kx is the horizontal component of the wavenumber vector, ![]() is the
vertical-time-normalized component
of the wavenumber vector, and
is the
vertical-time-normalized component
of the wavenumber vector, and
![]() is the angular frequency, we can transform
equation (9) to
is the angular frequency, we can transform
equation (9) to
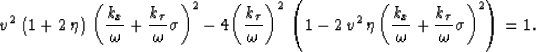
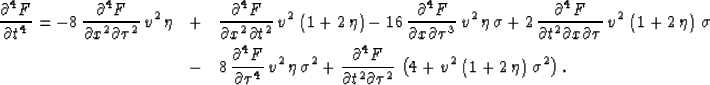
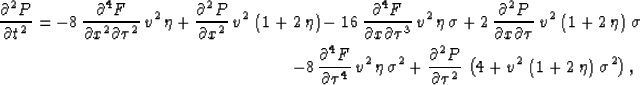
![]()
![]() -domain is clearly
independent of the vertical velocity when
-domain is clearly
independent of the vertical velocity when ![]() is given by equation 12 and
is given by equation 12 and
![]() is laterally invariant.
is laterally invariant.