Using the method of characteristics, we can derive a system of ordinary differential equations that define the ray trajectories. To do so, we need to transform equation (9) to the following form:
| |
(14) |
| |
(15) |
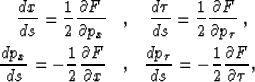 |
||
| (16) |
![]()
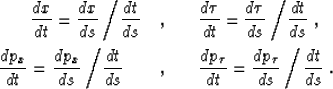 |
||
| (17) |
Using equation (9), we obtain
| |
(18) |
| (19) |
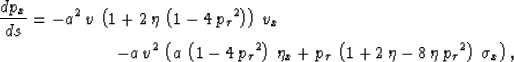 |
||
| (20) |
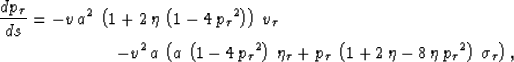 |
||
| (21) |
![]()
![]()
To trace rays, we must first
identify the initial values x0, ![]() , px0, and
, px0, and
![]() . The variables x0 and
. The variables x0 and
![]() describe the source position, and px0 and
describe the source position, and px0 and ![]() are extracted from the initial
angle of propagation. Note that, from equation (9),
are extracted from the initial
angle of propagation. Note that, from equation (9),
![]()
The raytracing system of equations (18-21)
describes the ray-theoretical aspect of wave propagation in the
![]() -domain, and can
be used as an alternative to the eikonal equation. Numerical solutions of the raytracing equations,
as opposed to the eikonal equation, provide multi-arrival traveltimes and amplitudes.
In the numerical examples,
we use raytracing to highlight some of the features of the
-domain, and can
be used as an alternative to the eikonal equation. Numerical solutions of the raytracing equations,
as opposed to the eikonal equation, provide multi-arrival traveltimes and amplitudes.
In the numerical examples,
we use raytracing to highlight some of the features of the ![]() -domain coordinate system.
-domain coordinate system.