




Next: Examples
Up: Fomel, et al.: Interpolation
Previous: Introduction
Claerbout (1992) formulates the basic principle of
missing data interpolation as follows:
A method for restoring missing data
is to ensure that the restored data,
after specified filtering,
has minimum energy.
Mathematically, this principle can be expressed by the simple equation
| 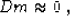 |
(1) |
where m is the data vector, and D is the specified filter. The
approximate equality sign means that equation (1) is
solved by minimizing the squared norm (the power) of its left side.
Additionally, the known data values must be preserved in the
optimization scheme. Introducing the mask operator K, which can be
considered as a diagonal matrix with zeros on the missing data
locations and ones elsewhere, we can rewrite equation
(1) in the more rigorous form
| 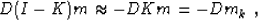 |
(2) |
in which I is the identity operator, and mk is the known portion
of the data. It is important to note that equation (2)
corresponds to the limiting case of the regularized linear system
| 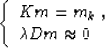 |
(3) |
for the scaling coefficient 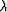 approaching zero. This means
that we put far more weight on the first equation in (3)
and use the second equation only to constrain the null space of the
solution. Applying the general theory of data-space regularization
Fomel (1997), one can immediately transform system
(3) to the equation
approaching zero. This means
that we put far more weight on the first equation in (3)
and use the second equation only to constrain the null space of the
solution. Applying the general theory of data-space regularization
Fomel (1997), one can immediately transform system
(3) to the equation
| 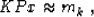 |
(4) |
where P is a preconditioning operator, and x is a new variable,
connected with m by the simple relationship
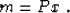
In theory, equations (4) and (2) have
exactly the same solutions if the following condition is satisfied:
| 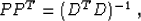 |
(5) |
where we need to assume the self-adjoint operator DT D to be
invertible. If D is represented by a discrete convolution, the
natural choice for P is the corresponding deconvolution operator:
| 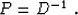 |
(6) |
The helix transform provides a constructive way of implementing
multidimensional deconvolution by one-dimensional recursive filtering.





Next: Examples
Up: Fomel, et al.: Interpolation
Previous: Introduction
Stanford Exploration Project
9/12/2000
![]()