




Next: About this document ...
Up: Fomel: Linearized Eikonal
Previous: A SIMPLE derivation of
The eikonal equation (1) can be rewritten in the form
| 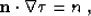 |
(12) |
where 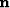 is the unit vector, pointing in the traveltime
gradient direction. The integral solution of equation (12)
takes the form
is the unit vector, pointing in the traveltime
gradient direction. The integral solution of equation (12)
takes the form
| 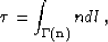 |
(13) |
which states that the traveltime  can be computed by
integrating the slowness n along the ray
can be computed by
integrating the slowness n along the ray 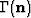 ,tangent at every point to the gradient direction
,tangent at every point to the gradient direction 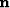 .
.
Similarly, we can rewrite the linearized eikonal equation (5)
in the form
| 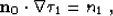 |
(14) |
where 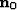 is the unit vector, pointing in gradient
direction for the initial traveltime
is the unit vector, pointing in gradient
direction for the initial traveltime 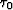 . The integral solution
of equation (14) takes the form
. The integral solution
of equation (14) takes the form
| 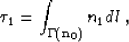 |
(15) |
which states that the traveltime perturbation 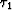 can be
computed by integrating the slowness perturbation n1 along the
ray
can be
computed by integrating the slowness perturbation n1 along the
ray 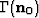 , defined by the initial slowness model
n0 . This is exactly the basic principle of traveltime
tomography.
, defined by the initial slowness model
n0 . This is exactly the basic principle of traveltime
tomography.
I have borrowed this proof from Lavrentiev et al. (1970), who used linearization
of the eikonal equation as the theoretical basis for traveltime inversion.





Next: About this document ...
Up: Fomel: Linearized Eikonal
Previous: A SIMPLE derivation of
Stanford Exploration Project
9/12/2000