




Next: A discretization scheme and
Up: Sava & Fomel: Huygens
Previous: Introduction
The eikonal equation, governing the traveltimes from a fixed source in
an isotropic heterogeneous medium, has the form
| 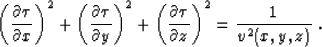 |
(1) |
Here x, y, and z are spatial coordinates,  is the
traveltime (eikonal), and v stands for the velocity field.
Constant-traveltime contours in the traveltime field
is the
traveltime (eikonal), and v stands for the velocity field.
Constant-traveltime contours in the traveltime field 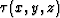 ,constrained by equation (1) and appropriate boundary
conditions, correspond to wavefronts of the propagating wave.
Additionally, each point on a wavefront can be parameterized by an
arbitrarily chosen ray parameter
,constrained by equation (1) and appropriate boundary
conditions, correspond to wavefronts of the propagating wave.
Additionally, each point on a wavefront can be parameterized by an
arbitrarily chosen ray parameter 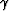 . In three dimensions,
. In three dimensions, 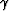 includes a pair of independent parameters. For brevity, from now on we
will restrict the analysis to two dimensions. One can easily generalize
it to the 3-D case by considering
includes a pair of independent parameters. For brevity, from now on we
will restrict the analysis to two dimensions. One can easily generalize
it to the 3-D case by considering 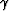 and x as vector quantities.
Thus, we will refer to the following two-dimensional form of equation
(1):
and x as vector quantities.
Thus, we will refer to the following two-dimensional form of equation
(1):
| 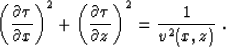 |
(2) |
For a point source, 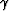 can be chosen as the initial ray angle at
the source. Zhang (1993) shows that
can be chosen as the initial ray angle at
the source. Zhang (1993) shows that 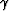 as a
function of spatial coordinates satisfies the simple partial
differential equation
as a
function of spatial coordinates satisfies the simple partial
differential equation
| 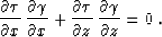 |
(3) |
Equation (3) merely expresses the fact that in an
isotropic medium, rays are locally orthogonal to wavefronts. The field
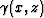 has not only theoretical interest as it provides one of
the possible ways for evaluating propagation amplitudes. In particular,
the geometrical spreading factor J (x,z) is connected to
has not only theoretical interest as it provides one of
the possible ways for evaluating propagation amplitudes. In particular,
the geometrical spreading factor J (x,z) is connected to 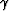 by
the simple relationship Zhang (1993)
by
the simple relationship Zhang (1993)
| 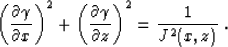 |
(4) |
It is important to note that for complex velocity fields, both  and
and 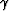 as functions of x and z become multi-valued. In this
case, the multi-valued character of the ray parameter
as functions of x and z become multi-valued. In this
case, the multi-valued character of the ray parameter 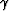 corresponds to the situation, where more than one ray from the source
passes through a particular point
corresponds to the situation, where more than one ray from the source
passes through a particular point 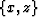 in the subsurface. This
situation presents a very difficult problem when equations
(2) and (3) are solved numerically.
Typically, only the first-arrival branch of the traveltime is picked
in the numerical calculation. The ray tracing method is free from that
limitation because it operates in the ray coordinate system. Ray
tracing computes the traveltime
in the subsurface. This
situation presents a very difficult problem when equations
(2) and (3) are solved numerically.
Typically, only the first-arrival branch of the traveltime is picked
in the numerical calculation. The ray tracing method is free from that
limitation because it operates in the ray coordinate system. Ray
tracing computes the traveltime  and the corresponding ray
positions x and z for a fixed ray parameter
and the corresponding ray
positions x and z for a fixed ray parameter 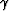 .
.
Since 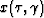 and
and 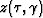 are uniquely defined for
arbitrarily complex velocity fields, we can now make an important
mathematical transformation. Considering equations (2) and
(3) as a system and applying the general rules of calculus,
we can transform this system by substituting the inverse functions
are uniquely defined for
arbitrarily complex velocity fields, we can now make an important
mathematical transformation. Considering equations (2) and
(3) as a system and applying the general rules of calculus,
we can transform this system by substituting the inverse functions
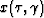 and
and 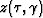 for the original fields
for the original fields
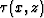 and
and 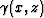 . The resultant expressions take the form
. The resultant expressions take the form
| 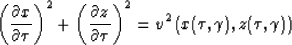 |
(5) |
and
| 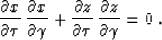 |
(6) |
Comparing equations (5) and (6) with the original
system (2-3) shows that equations (5)
and (6) again represent the dependence of ray coordinates and
Cartesian coordinates in the form of partial differential equations.
However, the solutions of system (5-6) are better
behaved and have a unique value for every  and
and 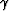 . These values
can be computed with the conventional ray tracing. However, the ray-tracing
approach is based on a system of ordinary differential equations, which
represents a different mathematical model.
. These values
can be computed with the conventional ray tracing. However, the ray-tracing
approach is based on a system of ordinary differential equations, which
represents a different mathematical model.
We use equations (5) and (6) as the basis of our
wavefront tracing algorithm. The next section discusses the discretization of
the differential equations and the physical interpretation we have given to
the scheme.





Next: A discretization scheme and
Up: Sava & Fomel: Huygens
Previous: Introduction
Stanford Exploration Project
9/12/2000
![]() can be chosen as the initial ray angle at
the source. Zhang (1993) shows that
can be chosen as the initial ray angle at
the source. Zhang (1993) shows that ![]() as a
function of spatial coordinates satisfies the simple partial
differential equation
as a
function of spatial coordinates satisfies the simple partial
differential equation
![]() and
and ![]() are uniquely defined for
arbitrarily complex velocity fields, we can now make an important
mathematical transformation. Considering equations (2) and
(3) as a system and applying the general rules of calculus,
we can transform this system by substituting the inverse functions
are uniquely defined for
arbitrarily complex velocity fields, we can now make an important
mathematical transformation. Considering equations (2) and
(3) as a system and applying the general rules of calculus,
we can transform this system by substituting the inverse functions
![]() and
and ![]() for the original fields
for the original fields
![]() and
and ![]() . The resultant expressions take the form
. The resultant expressions take the form
![]() and
and ![]() . These values
can be computed with the conventional ray tracing. However, the ray-tracing
approach is based on a system of ordinary differential equations, which
represents a different mathematical model.
. These values
can be computed with the conventional ray tracing. However, the ray-tracing
approach is based on a system of ordinary differential equations, which
represents a different mathematical model.