Causal and leaky integration

Causal integration in the continuous world is defined as  

$$y(t) \;=\; \int_{-\infty}^t \ x(t)\ dt\;.$$ (1)

A more general operator is leaky integration, defined as  

$$y(t) \;=\; \int_0^\infty \ x(t-\tau)\ e^{-\alpha\tau} \ d\tau\;.$$ (2)

As $\alpha \rightarrow 0$, leaky integration becomes causal integration. An efficient numerical implementation of a simple causal integrator employs the fact that operator (1) solves the differential equation  

$$dy/dt=x(t)\;,$$ (3)

and operator (2) solves  

$$dy/dt=\alpha\,y(t) + x(t)\;.$$ (4)

In the discrete world, equation (4) leads to the recursion scheme  

$$y_t \;=\; \rho\; y_{t-1} + x_t \quad \quad \quad t\ {\rm increasing}\;,$$ (5)

where $\rho = 1$ for $\alpha = 0$.The adjoint of (5) is the recursion  

$$\tilde x_{t-1} \;=\; \rho \tilde x_{t} + y_{t-1} \quad \quad \quad t \ {\rm decreasing}\;,$$ (6)

which corresponds to anticausal leaky integration  

$$\tilde x(t) \;=\; \int_0^\infty \ y(\tau-t)\ e^{-\alpha\tau} \ d\tau\;.$$ (7)

Module leakint implements causal and anticausal integration.

module leakint
  use adj_mod

real, private :: r = 1.

contains

subroutine leakint_init (rho)
    real, intent (in) :: rho
    r = rho
  end subroutine leakint_init

function leakint_op (adj, add, x, y) result (stat)
    integer              :: stat
    logical, intent (in) :: adj, add
    real, dimension (:)  :: x, y

call adjnull (adj, add, x, y)

if (adj) then
       call integrate (y,size (y),1,x)
    else
       call integrate (x,1,size (x),y)
    end if

stat = 0

contains

subroutine integrate (inp, nb, ne, out)
      integer,             intent (in)  :: nb, ne
      real, dimension (:), intent (in)  :: inp
      real, dimension (:), intent (out) :: out

integer                           :: i
      real                              :: t

t = 0.
      do i = nb, ne, sign (1, ne - nb)
         t = r * t + inp (i)
         out (i) = out (i) + t
      end do
    end subroutine integrate

end function leakint_op

end module leakint

The operator function leakint_op contains and calls the helper subroutine integrate, which implements recusions (5) and (6). Figure 2 illustrates the program for $\rho = 1$.

 

causint90 Figure 2 in1 is an input pulse. C in1 is its causal integral. C' in1 is the anticausal integral of the pulse. in2 is a separated doublet. Its causal integration is a box and its anticausal integration is the negative. CC in2 is the double causal integral of in2.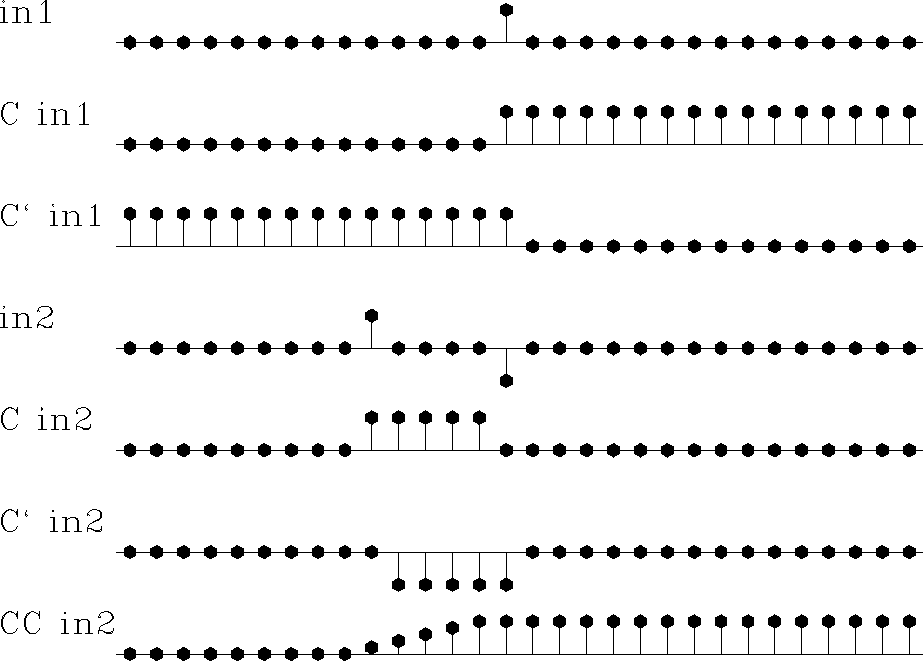