|
fermat
Figure 2 Illustration of the connection between Fermat's principle and the eikonal equation. The shortest distance between a wavefront and a neighboring point M is along the wavefront normal. | 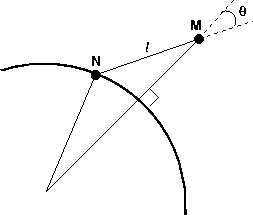 |
This section serves as a brief reminder of the well-known theoretical connection between Fermat's principle and the eikonal equation. The reader, familiar with this theory, can skip safely to the next section.
|
fermat
Figure 2 Illustration of the connection between Fermat's principle and the eikonal equation. The shortest distance between a wavefront and a neighboring point M is along the wavefront normal. |  |
Both Fermat's principle and the eikonal equation can serve as the foundation of traveltime calculations. In fact, either one can be rigorously derived from the other. A simplified derivation of this fact is illustrated in Figure 2. Following the notation of this figure, let us consider a point M in the immediate neighborhood of a wavefront t (N) = tN. Assuming that the source is on the other side of the wavefront, we can express the traveltime at the point M as the sum
| |
(3) |
| |
(4) |
If we accept the local Fermat's principle, which says that the ray
from the source to M corresponds to the minimum-arrival time, then,
as we can see geometrically from Figure 2, the angle
![]() in formula (4) should be set to zero to achieve
the minimum. This conclusion leads directly to the eikonal equation
(2). On the other hand, if we start from the eikonal
equation, then it also follows that
in formula (4) should be set to zero to achieve
the minimum. This conclusion leads directly to the eikonal equation
(2). On the other hand, if we start from the eikonal
equation, then it also follows that ![]() , which corresponds to
the minimum traveltime and constitutes the local Fermat's principle.
The idea of that simplified proof is taken from Lanczos (1966),
though it has obviously appeared in many other publications. The
situations in which the wavefront surface has a discontinuous normal
(given raise to multiple-arrival traveltimes) require a more elaborate
argument, but the above proof does work for first-arrival traveltimes
and the corresponding viscosity solutions of the eikonal equation
Lions (1982).
, which corresponds to
the minimum traveltime and constitutes the local Fermat's principle.
The idea of that simplified proof is taken from Lanczos (1966),
though it has obviously appeared in many other publications. The
situations in which the wavefront surface has a discontinuous normal
(given raise to multiple-arrival traveltimes) require a more elaborate
argument, but the above proof does work for first-arrival traveltimes
and the corresponding viscosity solutions of the eikonal equation
Lions (1982).
The connection between variational principles and first-order partial-differential equations has a very general meaning, explained by the classic Hamilton-Jacobi theory. One generalization of the eikonal equation is
| |
(5) |
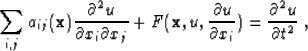 |
(6) |
A known theorem Smirnov (1964) states that the propagation rays [characteristics of equation (5) and, correspondingly, bi-characteristics of equation (6)] are geodesic (extreme-length) curves in the Riemannian metric
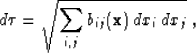 |
(7) |
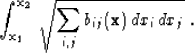
| |
(8) |
From equation (7), we see that Fermat's principle in the general variational formulation applies to a much wider class of situations if we interpret it with the help of non-Euclidean geometries.