A brief description of the fast marching method

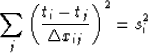
For a detailed description of level set methods, the reader is referred to Sethian's recently published book 1996b. More details on the fast marching method appear in articles by Sethian (1996a) and Sethian and Popovici (1997). This section serves as a brief introduction to the main bulk of the algorithm.

The key feature of the algorithm is a carefully selected order of traveltime evaluation. At each step of the algorithm, every grid point is marked as either Alive (already computed), NarrowBand (at the wavefront, pending evaluation), or FarAway (not touched yet). Initially, the source points are marked as Alive , and the traveltime at these points is set to zero. A continuous band of points around the source are marked as NarrowBand , and their traveltime values are computed analytically. All other points in the grid are marked as FarAway and have an ``infinitely large'' traveltime value.

An elementary step of the algorithm consists of the following moves:

1.

Among all the NarrowBand points, extract the point with the minimum traveltime.

2.

Mark this point as Alive .

3.

Check all the immediate neighbors of the minimum point and update them if necessary.

4.

Repeat.

An update procedure is based on an upwind first-order approximation to the eikonal equation. In simple terms, the procedure starts with selecting one or more (up to three) neighboring points around the updated point. The traveltime values at the selected neighboring points need to be smaller than the current value. After the selection, one solves the quadratic equation  

$$\sum_{j} \left(\frac{t_i-t_j}{\triangle x_{ij}}\right)^2 = s_i^2$$ (1)

for t_i. Here t_i is the updated value, t_j are traveltime values at the neighboring points, s_i is the slowness at the point i, and $\triangle x_{ij}$ is the grid size in the ij direction. As the result of the updating, either a FarAway point is marked as NarrowBand or a NarrowBand point gets assigned a new value.

Except for the updating scheme (1), the fast marching algorithm bears a very close resemblance to the famous shortest path algorithm of Dijkstra (1959). It is important to point out that unlike Moser's method, which uses Dijkstra's algorithm directly Moser (1991), the fast marching approach does not construct the ray paths from predefined pieces, but dynamically updates traveltimes according to the first-order difference operator (1). As a result, the computational error of this method goes to zero with the decrease in the grid size in a linear fashion. The proof of validity of the method (omitted here) is also analogous to that of Dijkstra's algorithm Sethian (1996a,b). As in most of the shortest-path implementations, the computational cost of extracting the minimum point at each step of the algorithm is greatly reduced [from O (N) to $O (\log N)$ operations] by maintaining a priority-queue structure (heap) for the NarrowBand points Cormen et al. (1990).

Figure 1 shows an example application of the fast marching eikonal solver on the three-dimensional SEG/EAGE salt model. The computation is stable despite the large velocity contrasts in the model. The current implementation takes about 10 seconds for computing a 100x100x100 grid on one node of SGI Origin 200. Alkhalifah and Fomel 1997 discuss the differences between Cartesian and polar coordinate implementations.

 

salt Figure 1 Constant-traveltime contours of the first-arrival traveltime, computed in the SEG/EAGE salt model. A point source is positioned inside the salt body. The top plot is a diagonal slice; the bottom plot, a depth slice.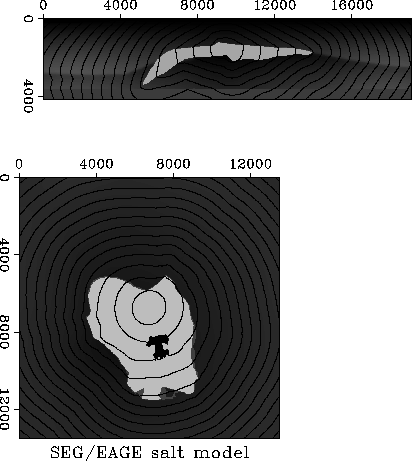

The difference equation (1) is a finite-difference approximation to the continuous eikonal equation  

$$\left(\frac{\partial t}{\partial x}\right)^2 + \left(\frac{\... ...+ \left(\frac{\partial t}{\partial z}\right)^2 = s^2 (x,y,z)\;,$$ (2)

where x, y, and z represent the spatial Cartesian coordinates. In the next two sections, I show how the updating procedure can be derived without referring to the eikonal equation, but with the direct use of Fermat's principle.