Next: About this document ...
Up: Fomel & Claerbout: Implicit
Previous: The 1/6-th trick
The problem of approximating the Laplacian operator in two dimensions
not only inherits the inaccuracies of the one-dimensional
finite-difference approximations, but also raises the issue of
azimuthal asymmetry. For example, the usual five-point filter
| 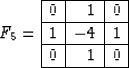 |
(26) |
exhibits a clear difference between the grid directions and the
directions at a 45-degree angle to the grid. To overcome this
unpleasant anisotropy, we can consider a slightly larger filter of the
form
| 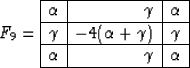 |
(27) |
where the constants  and
and  are to be defined. The
Fourier-domain representation of filter (27) is
are to be defined. The
Fourier-domain representation of filter (27) is
| ![\begin{displaymath}
F_9 (k_x,k_y) = 4\,\alpha\,[\cos{k_x}\,\cos{k_y} - 1] +
2\,\gamma\,[\cos{k_x}+\cos{k_y}-2]\;,\end{displaymath}](img64.gif) |
(28) |
and the isotropic filter that we can try to approximate is defined
analogously to its one-dimensional equivalent, as follows:
| 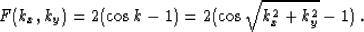 |
(29) |
Comparing equations (28) and (29), we notice that
they match exactly, when either of the wavenumbers kx or ky is
equal to zero, provided that
| 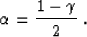 |
(30) |
Therefore, we can reduce the problem to estimating a single
coefficient 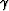 . Another way of expressing this conclusion is to
represent filter F9 in equation (28) as a linear
combination of filter F5 from equation (28) and its
rotated version Cole (1994), as follows:
. Another way of expressing this conclusion is to
represent filter F9 in equation (28) as a linear
combination of filter F5 from equation (28) and its
rotated version Cole (1994), as follows:
| 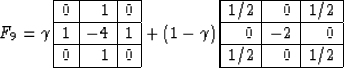 |
(31) |
With the value of 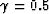 , filter F9 takes the value
, filter F9 takes the value
| 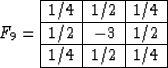 |
(32) |
and corresponds precisely to the nine-point McClellan filter
Hale (1991a); McClellan (1973). On the other hand, the value of
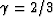 gives the least error in the vicinity of the zero
wavenumber k. In this case, the filter is
gives the least error in the vicinity of the zero
wavenumber k. In this case, the filter is
| 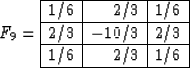 |
(33) |
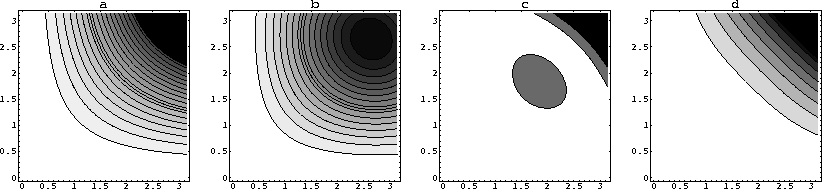
Errors of different approximations are plotted in Figure
11![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) laplace
laplace
Figure 11 The numerical anisotropy error of different
Laplacian approximations. Both the five-point Laplacian (plot a) and
its rotated version (plot b) are accurate along the axes, but
exhibit significant anisotropy in between at large wavenumbers. The
nine-point McClellan filter (plot c) has a reduced error, while the
filter with 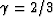 (plot d) has the flattest error around the
origin.
(plot d) has the flattest error around the
origin.





Under the helix transform, a filter of the general form
(27) becomes equivalent to a one-dimensional filter with
the Z transform
| 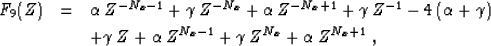 |
|
| (34) |
where Nx is the helix period (the number of grid points in the x
dimension). To find the inverse of a convolution with filter
(34), we factorize the filter into the causal minimum-phase
component and its adjoint:
| 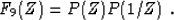 |
(35) |
To find the coefficients of the filter P, any one-dimensional
spectral factorization method can be applied. It is important to point
out that the result of factorization (neglecting the numerical errors)
does not depend on Nx. Another approach is to define a residual
error vector for the coefficients of Z in equation (35)
and minimize it for some particular norm. For example, minimizing the
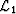 norm when F9 is the McClellan filter
(32), we discover that the filter P, after transforming
back to two dimensions, takes the form
norm when F9 is the McClellan filter
(32), we discover that the filter P, after transforming
back to two dimensions, takes the form
| 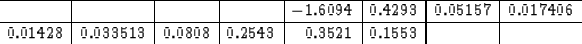 |
(36) |
The results of applying a recursive deconvolution with filter
(36) are shown in Figure 12. An
essentially similar procedure, only with a different set of filters,
works for implicit wavefield extrapolation.
inv-laplace
Figure 12 Inverting the Laplacian
operator by a helix deconvolution. The top left plot shows the
input, which contains a single spike and the causal minimum-phase
filter P. The top right plot is the result of inverse filtering.
As expected, the filter is deconvolved into a spike, and the spike
turns into a smooth one-sided impulse. After the second run, in the
backward (adjoint) direction, we obtain a numerical solution of
Laplace's equation! In the two bottom plots, the solution is shown
with grayscale and contours.










Next: About this document ...
Up: Fomel & Claerbout: Implicit
Previous: The 1/6-th trick
Stanford Exploration Project
9/12/2000
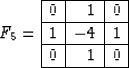
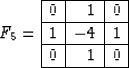
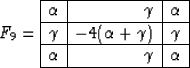
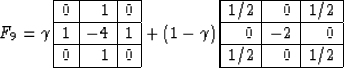
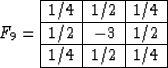
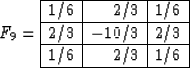
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)