




Next: Constructing an ``isotropic'' Laplacian
Up: Fomel & Claerbout: Implicit
Previous: REFERENCES
Given the filter D2 (k), defined in formula (10), we can
construct an accurate approximation to the second derivative operator
-k2 by considering a filter ratio (another Padé-type
approximation) of the form
| 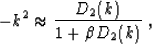 |
(25) |
where 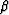 is an adjustable constant Claerbout (1985).
The actual Padé coefficient is
is an adjustable constant Claerbout (1985).
The actual Padé coefficient is 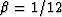 . As pointed out by
Francis Muir, the value of
. As pointed out by
Francis Muir, the value of 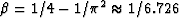 gives an exact fit at the Nyquist frequency
gives an exact fit at the Nyquist frequency 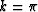 . Fitting the
derivative operator in the L1 norm yields the value of
. Fitting the
derivative operator in the L1 norm yields the value of 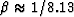 . All these approximations are shown in Figure
10.
. All these approximations are shown in Figure
10.
sixth
Figure 10 The second-derivative operator
in the wavenumber domain and its approximations.
|
|  |





B





Next: Constructing an ``isotropic'' Laplacian
Up: Fomel & Claerbout: Implicit
Previous: REFERENCES
Stanford Exploration Project
9/12/2000
