




Next: Second step of the
Up: IN SEARCH OF THE
Previous: IN SEARCH OF THE
Assuming n>1, we can add some
amount of the previous step 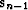 to the chosen direction
to the chosen direction
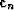 to produce a new search direction
to produce a new search direction 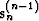 , as
follows:
, as
follows:
| 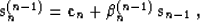 |
(10) |
where 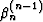 is an adjustable scalar coefficient. According to
to the fundamental orthogonality principle (7),
is an adjustable scalar coefficient. According to
to the fundamental orthogonality principle (7),
| 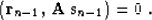 |
(11) |
As follows from equation (11), the numerator on the right-hand
side of equation (9) is not affected by the new choice of the
search direction:
| ![\begin{displaymath}
\left({\bf r}_{n-1},\,{\bf A\,s}_n^{(n-1)}\right)^2 = \left[...
...ight)\right]^2 =
\left({\bf r}_{n-1},\,{\bf A\,c}_n\right)^2\;.\end{displaymath}](img27.gif) |
(12) |
However, we can use transformation (10) to decrease the
denominator in (9), thus further decreasing the residual
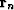 . We achieve the minimization of the denominator
. We achieve the minimization of the denominator
| 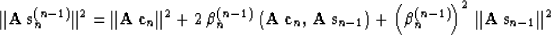 |
(13) |
by choosing the coefficient 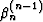 to be
to be
| 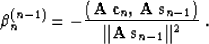 |
(14) |
Note the analogy between (14) and (6). Analogously to
(7), equation (14) is equivalent to the orthogonality condition
| 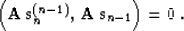 |
(15) |
Analogously to (8), applying formula (14) is also equivalent to defining the
minimized denominator as
| 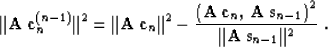 |
(16) |





Next: Second step of the
Up: IN SEARCH OF THE
Previous: IN SEARCH OF THE
Stanford Exploration Project
9/11/2000