Example 1: Inverse interpolation

Matthias Schwab has suggested (in a personal communication) an interesting example, in which the cgstep program fails to comply with the conjugate-gradient theory. The inverse problem is a simple one-dimensional data interpolation with a known filter Claerbout (1994). The known portion of the data is a single spike in the middle. One hundred other data points are considered missing. The known filter is the Laplacian (1,-2,1), and the expected result is a bell-shaped cubic spline. The forward problem is strictly linear, and the exact adjoint is easily computed by reverse convolution. 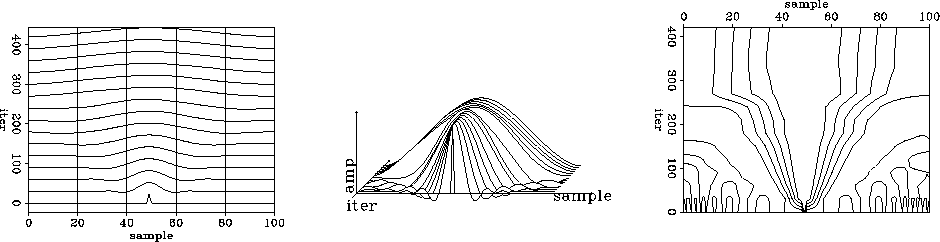However, the conjugate-gradient program requires significantly more than the theoretically predicted 100 iterations. Figure 2 displays the convergence to the final solution in three different plots. 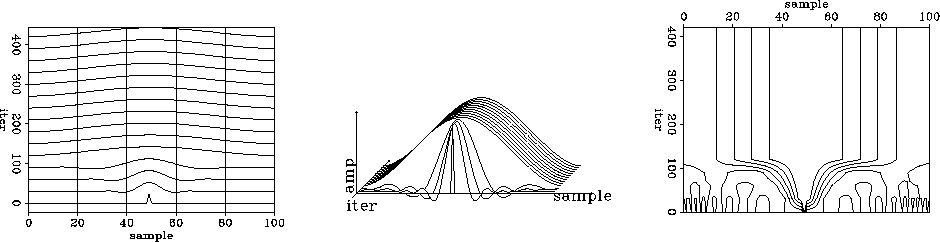According to the figure, the actual number of iterations required for convergence is about 300. Figure 3 shows the result of a similar experiment with the conjugate-direction solver cdstep. The number of required iterations is reduced to almost the theoretical one hundred. This indicates that the orthogonality of directions implied in the conjugate-gradient method has been distorted by computational errors. The additional cost of correcting these errors with the conjugate-direction solver comes from storing the preceding 100 directions in memory. A smaller number of memorized steps produces smaller improvements.

 

dirmcg
Figure 2 Convergence of the missing data interpolation problem with the conjugate-gradient solver. Current models are plotted against the number of iterations. The three plots are different displays of the same data.

 

dirmcd
Figure 3 Convergence of the missing data interpolation problem with the long-memory conjugate-direction solver. Current models are plotted against the number of iterations. The three plots are different displays of the same data.