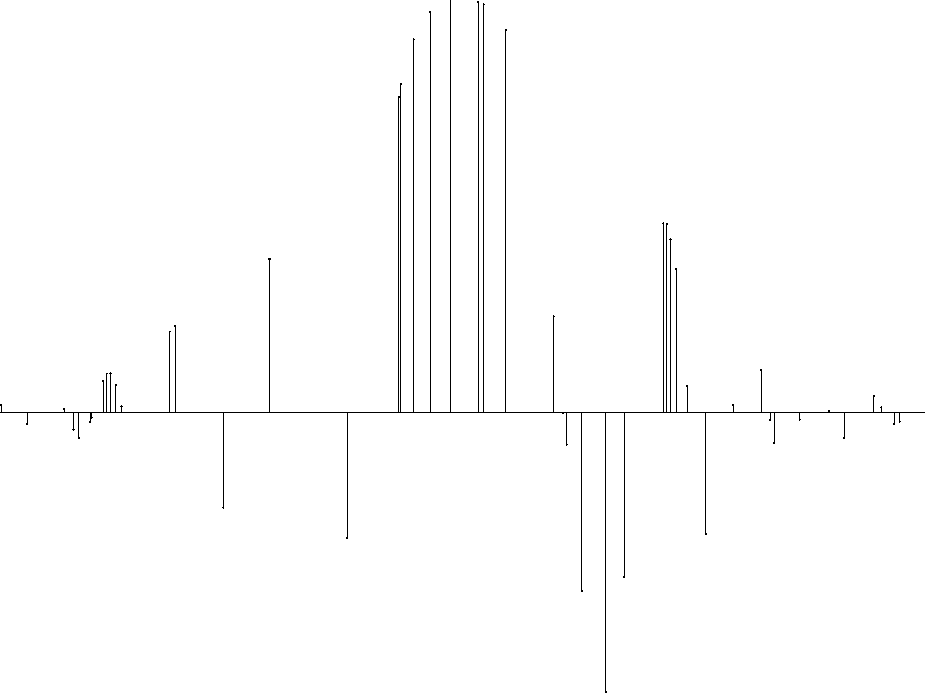Next: Application to 3-D seismic
Up: Inverse Interpolation and Data
Previous: Spline regularization
Now that we have all the problem pieces together, we can test the
performance gain in the inverse interpolation
problem (19)-(25) from the application of B-splines.
For a simple 1-D test, I chose the function shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , but sampled at irregular locations. To create two
different regimes for the inverse interpolation problem, I chose 50
and 500 random locations. The two sets of points were interpolated to
500 and 50 regular samples respectively. The first test corresponds to
an under-determined situation, while the second test is clearly
over-determined. Figures
, but sampled at irregular locations. To create two
different regimes for the inverse interpolation problem, I chose 50
and 500 random locations. The two sets of points were interpolated to
500 and 50 regular samples respectively. The first test corresponds to
an under-determined situation, while the second test is clearly
over-determined. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the
input data for the two test after normalized binning to the selected
regular bins.
show the
input data for the two test after normalized binning to the selected
regular bins.
bin500
Figure 29 50 random points binned to 500 regular
grid points. The random data are used for testing inverse
interpolation in an under-determined situation.
|
| 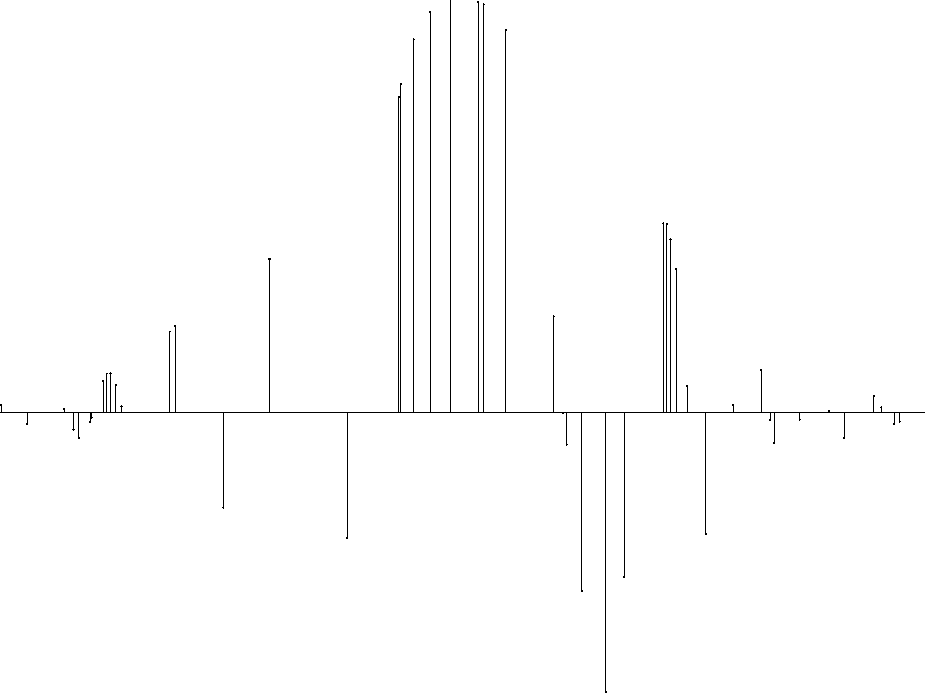 |





bin50
Figure 30 500 random points binned to 50 regular
grid points. The random data are used for testing inverse
interpolation in an over-determined situation.
|
|  |





I solved system (19)-(25) by the iterative
conjugate-gradient method, utilizing a recursive filter
preconditioning Fomel (1997a) for faster convergence.
The regularization operator  was constructed by using the
method of the previous subsection with the tension-spline differential
equation Fomel (2000b); Smith and Wessel (1990) and the
tension parameter of 0.01.
was constructed by using the
method of the previous subsection with the tension-spline differential
equation Fomel (2000b); Smith and Wessel (1990) and the
tension parameter of 0.01.
The least-squares differences between the true and the estimated model
are plotted in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
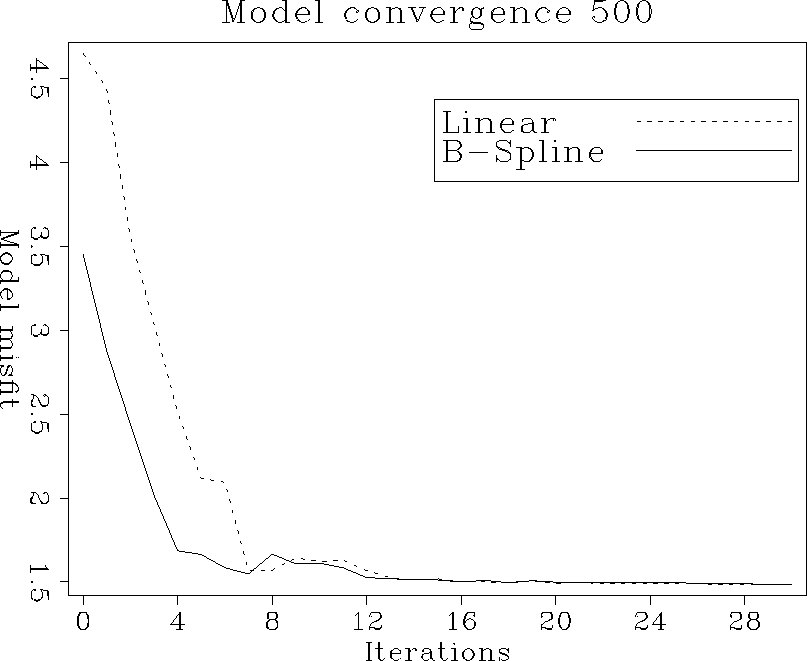
Observing the behavior of the model misfit versus the number of
iterations and comparing simple linear interpolation with the
third-order B-spline interpolation, we discover that
.
Observing the behavior of the model misfit versus the number of
iterations and comparing simple linear interpolation with the
third-order B-spline interpolation, we discover that
- In the under-determined case, both methods converge to the same
final estimate, but B-spline inverse interpolation does it faster at
earlier iterations. The total computational gain is not significant,
because each B-spline iteration is more expensive than the
corresponding linear interpolation iteration.
- In the over-determined case, both methods converge similarly at
early iterations, but B-spline inverse interpolation results in a
more accurate final estimate.
From the results of this simple experiment, it is apparent that the
main advantage of using more accurate interpolation in the data
regularization context occurs in the over-determined situation, when
the estimated model is well constrained by the available data.
norm500
Figure 31 Model convergence in the
under-determined case. Dashed line: using linear
interpolation. Solid line: using third-order B-spline.
|
|  |





norm50
Figure 32 Model convergence in the
over-determined case. Dashed line: using linear
interpolation. Solid line: using third-order B-spline.
|
|  |










Next: Application to 3-D seismic
Up: Inverse Interpolation and Data
Previous: Spline regularization
Stanford Exploration Project
11/9/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , but sampled at irregular locations. To create two
different regimes for the inverse interpolation problem, I chose 50
and 500 random locations. The two sets of points were interpolated to
500 and 50 regular samples respectively. The first test corresponds to
an under-determined situation, while the second test is clearly
over-determined. Figures
, but sampled at irregular locations. To create two
different regimes for the inverse interpolation problem, I chose 50
and 500 random locations. The two sets of points were interpolated to
500 and 50 regular samples respectively. The first test corresponds to
an under-determined situation, while the second test is clearly
over-determined. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the
input data for the two test after normalized binning to the selected
regular bins.
show the
input data for the two test after normalized binning to the selected
regular bins.