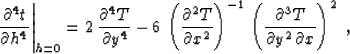Next: About this document ...
Up: Fomel & Grechka: Nonhyperbolic
Previous: REFERENCES
In this Appendix, we derive formulas that relate traveltime
derivatives of the reflected wave, evaluated at the zero offset point,
and traveltime derivatives of the direct wave, evaluated in the
vicinity of the zero-offset (central) ray. Such a relationship for
second-order derivatives is known as the NIP (normal incidence point)
theorem Chernjak and Gritsenko (1979); Hubral and Krey (1980); Hubral (1983). Its extension to
high-order derivatives is described by Fomel 1994.
Reflection traveltime in any type of model can be considered as a
function of the source and receiver locations s and r and the
location of the reflection point x, as follows:
| 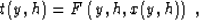 |
(90) |
where y is the midpoint 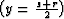 , h is
the half-offset
, h is
the half-offset 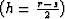 , and the
function F has a natural decomposition into two parts corresponding
to the incident and reflected rays:
, and the
function F has a natural decomposition into two parts corresponding
to the incident and reflected rays:
| 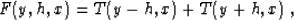 |
(91) |
where T is the traveltime of the direct wave. Clearly, at the
zero-offset point,
| 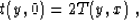 |
(92) |
where x=x(y,0) corresponds to the reflection point of the central
ray.
Differentiating formula (90) with respect to the half-offset
h and applying the chain rule, we obtain
| 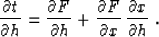 |
(93) |
According to Fermat's principle, one of the
fundamental principles of ray theory, the ray
trajectory of the reflected wave corresponds to an
extremum value of the traveltime. Parameterizing
the trajectory in terms of the reflection point
location x and assuming that F is a smooth
function of x, we can write Fermat's principle
in the form
| 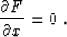 |
(94) |
Equation (94) must be satisfied for any values of x and
h. Substituting this equation into formula (93) leads to the
equation
| 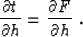 |
(95) |
Differentiating (95) again with respect to h, we arrive at the
formula
| 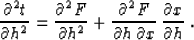 |
(96) |
Interchanging the source and receiver locations doesn't change the
reflection point position (the principle of reciprocity). Therefore,
x is an even function of the offset h, and we can simplify formula
(96) at zero offset, as follows:
| 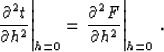 |
(97) |
Substituting the expression for the function F (91) into
(97) leads to the equation
| 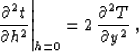 |
(98) |
which is the mathematical formulation of the NIP
theorem. It proves that the second-order
derivative of the reflection traveltime with
respect to the offset is equal, at zero offset,
to the second derivative of the direct wave
traveltime for the wave propagating from the
incidence point of the central ray. One immediate
conclusion from the NIP theorem is that the
short-spread normal moveout velocity, connected
with the derivative in the left-hand-side of
equation (98) can depend on the reflector
dip but doesn't depend on the curvature of the
reflector. Our derivation up to this point has
followed the derivation suggested by Chernjak and
Gritsenko 1979.
Differentiating formula (96) twice with respect to h evaluates,
with the help of the chain rule, the fourth-order derivative, as
follows:
| 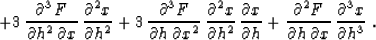 |
(99) |
Again, we can apply the principle of reciprocity to eliminate the
odd-order derivatives of x in formula (99) at the zero
offset. The resultant expression has the form
| 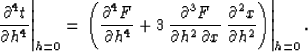 |
(100) |
In order to determine the unknown second derivative of the reflection
point location 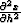 , we
differentiate Fermat's equation (94) twice, obtaining
, we
differentiate Fermat's equation (94) twice, obtaining
| 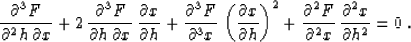 |
(101) |
Simplifying this equation at zero offset, we can solve it for the
second derivative of x. The solution has the form
| ![\begin{displaymath}
\left.{{\partial^2 x} \over {\partial h^2}}\right\vert _{h=0...
...\partial^3 F} \over {\partial^2 h\,\partial x}}\right]_{h=0}\;.\end{displaymath}](img126.gif) |
(102) |
Here we neglect the case of 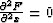 , which corresponds to a focusing of the reflected rays at the
surface. Finally, substituting expression (102) into (100)
and recalling the definition of the F function
from (91), we obtain
the equation
, which corresponds to a focusing of the reflected rays at the
surface. Finally, substituting expression (102) into (100)
and recalling the definition of the F function
from (91), we obtain
the equation
| 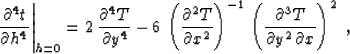 |
(103) |
which is the same as equation (74) in the main
text. Higher-order derivatives can be expressed in an analogous way
with a set of recursive algebraic functions Fomel (1994).
In the derivation of formulas (98) and (103), we have used
Fermat's principle, the principle of reciprocity, and the rules of
calculus. Both these formulas remain valid in anisotropic media as
well as in heterogeneous media, providing that the traveltime function
is smooth and that focusing of the reflected rays doesn't occur at the
surface of observation.





Next: About this document ...
Up: Fomel & Grechka: Nonhyperbolic
Previous: REFERENCES
Stanford Exploration Project
9/12/2000
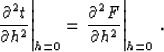
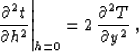
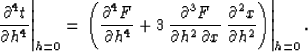
![\begin{displaymath}
\left.{{\partial^2 x} \over {\partial h^2}}\right\vert _{h=0...
...\partial^3 F} \over {\partial^2 h\,\partial x}}\right]_{h=0}\;.\end{displaymath}](img126.gif)