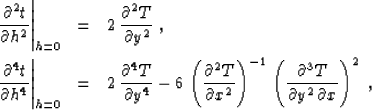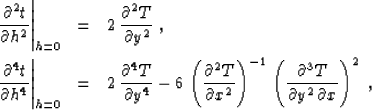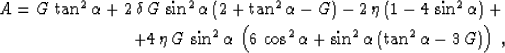Next: TI MOVEOUT IN TERMS
Up: CURVILINEAR REFLECTOR
Previous: Isotropic case
In the case of a dipping curved reflector in a homogeneous VTI medium,
the ray trajectories of the incident and reflected waves are straight,
but the location of the reflection point is no longer controlled by
the isotropic laws. In order to obtain analytic expressions for this
case, we use the theorem, which connects the derivatives of the
common-midpoint traveltime curves with the derivatives of the forward
traveltimes for the imaginary wave originating at the reflection point
of the central ray. This theorem has been introduced for the
second-order derivatives by Chernjak and Gritsenko 1979
and is usually referred to as the normal incidence point (NIP) theorem
Hubral and Krey (1980); Hubral (1983). Though the original proof didn't address the
case of anisotropy, it is applicable to this case as well, being based
on the fundamental Fermat's principle. The normal incidence point in
the anisotropic case should be replaced by the point of incidence for
the central ray (which is in general not normal to the reflector
surface). In the appendix, we review the NIP theorem as well as its
extension for high-order traveltime derivatives Fomel (1994).
Two basis formulas derived in the appendix take the following form:
| 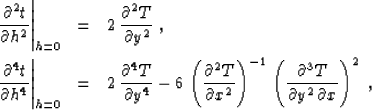 |
(73) |
| (74) |
where T(x,y) is the traveltime of the direct wave propagating from
the reflector point x to the point y at the surface z=0. All the
derivatives in formulas (73) and (74) are evaluated in the
vicinity of the central (zero-offset) ray. Both formulas are based
solely on Fermat's principle and therefore remain valid in any type of
medium for reflectors of arbitrary shape, assuming that the traveltimes
possess the required order of smoothness. It is especially convenient
to use formulas (73) and (74) in the case of homogeneous
media, because the forward traveltime in this case has an explicit
expression.
In order to apply formulas (73) and (74) to the VTI case,
we need to start by tracing the central ray. According to Fermat's
principle, the ray trajectory must correspond to the extremum value of
the traveltime. For the central ray, this simply means that in the
vicinity of the central ray, the traveltime of the direct ray
satisfies the equation
| 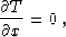 |
(75) |
where
| 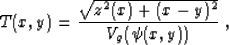 |
(76) |
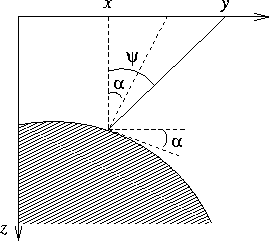
z(x) describes the reflector surface, and 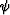 is the ray angle,
which satisfies the evident trigonometric relationship (see Figure
5)
is the ray angle,
which satisfies the evident trigonometric relationship (see Figure
5)
| 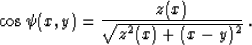 |
(77) |
Substituting approximate equation (9) for the group velocity
Vg into formula (76) and linearizing with respect to the
anisotropic parameters 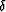 and
and  , we can solve equation
(75) for y, obtaining
, we can solve equation
(75) for y, obtaining
| 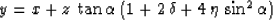 |
(78) |
or, in other terms,
| 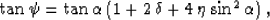 |
(79) |
where  is the local dip angle of the reflector at the
reflection point x. Equation (79) clearly shows that in VTI
media the central ray angle
is the local dip angle of the reflector at the
reflection point x. Equation (79) clearly shows that in VTI
media the central ray angle 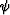 differs from the dip angle
differs from the dip angle
 . As one can expect, the difference is approximately
proportional to Thomsen's anisotropic parameters.
. As one can expect, the difference is approximately
proportional to Thomsen's anisotropic parameters.
nmoray
Figure 5 Zero-offset reflection from a
curved reflector in a VTI medium (a scheme). Note that the ray angle
is not equal to the local dip angle.
|
|  |

Now we can apply formula (73) to evaluate the second term of the
Taylor series expansion (26) for the case of a curved
reflector. The linearization in anisotropic parameters in this case
leads to the expression
| 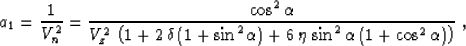 |
(80) |
which is equivalent to Tsvankin's result Tsvankin (1995). As in the
isotropic case, the normal moveout velocity does not depend on the
curvature. Its dip dependence is an important indicator of anisotropy,
especially in areas of conflicting dips Alkhalifah and Tsvankin (1995).
Finally, we can apply formula (74) to determine the third
coefficient of the Taylor series. After linearization in anisotropic
parameters and lengthy algebra, the resulting expression takes the
form
| 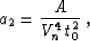 |
(81) |
where
| 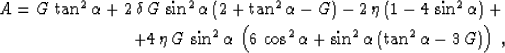 |
|
| (82) |
and the coefficient G is defined by equation (65). In the case of
a zero curvature (a plane reflector), G is also equal to zero, and
the only term remaining in formula (82) is
| 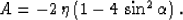 |
(83) |
In the general case of a curved reflector, we can rewrite the
isotropic formula (70) in the form
| 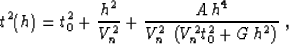 |
(84) |
where the normal moveout velocity Vn is given by
(80). Equation (84) approximates nonhyperbolic
moveouts in a VTI medium with a curved reflector. In the isotropic
case, it reduces to formula (70). In the case of a small
curvature, the accuracy of formula (84) at finite offsets
can be increased by modifying the denominator term.





Next: TI MOVEOUT IN TERMS
Up: CURVILINEAR REFLECTOR
Previous: Isotropic case
Stanford Exploration Project
9/12/2000