Tutorial Kirchhoff code

Subroutine kirchslow() below is the best tutorial Kirchhoff migration-modeling program I could devise. Think of data as a function of traveltime t and the horizontal axis x. Think of model (or image) as a function of traveltime t and the horizontal axis x. The program copies information from data space data(it,iy) to model space modl(iz,ix) or vice versa.

Data space and model space each have two axes. Of the four axes, three are independent (stated by loops) and the fourth is derived by the circle-hyperbola relation $t^2=\tau^2+x^2/v^2$.Subroutine kirchslow() for adj=0 copies information from model space to data space, i.e. from the hyperbola top to its flanks. For adj=1, data summed over the hyperbola flanks is put at the hyperbola top.

 

# Kirchhoff migration and diffraction.  (tutorial, slow)
#
subroutine kirchslow(   adj, add,  velhalf, t0,dt,dx, modl,nt,nx,  data)
integer ix,iy,it,iz,nz, adj, add,                          nt,nx
real x0,y0,dy,z0,dz,t,x,y,z,hs,    velhalf, t0,dt,dx, modl(nt,nx), data(nt,nx)
call adjnull(           adj, add,                     modl,nt*nx,  data,nt*nx)
x0=0.;  y0=0;  dy=dx;  z0=t0;  dz=dt; nz=nt
do ix= 1, nx {  x = x0 + dx * (ix-1)
do iy= 1, nx {  y = y0 + dy * (iy-1)
do iz= 1, nz {  z = z0 + dz * (iz-1)            # z = travel-time depth
        hs=      (x-y) / velhalf
        t = sqrt( z * z  +  hs * hs )
        it = 1.5 + (t-t0) / dt
        if( it <= nt )
                if( adj == 0 )
                        data(it,iy) = data(it,iy) + modl(iz,ix)
                else
                        modl(iz,ix) = modl(iz,ix) + data(it,iy)
        }}}
return; end

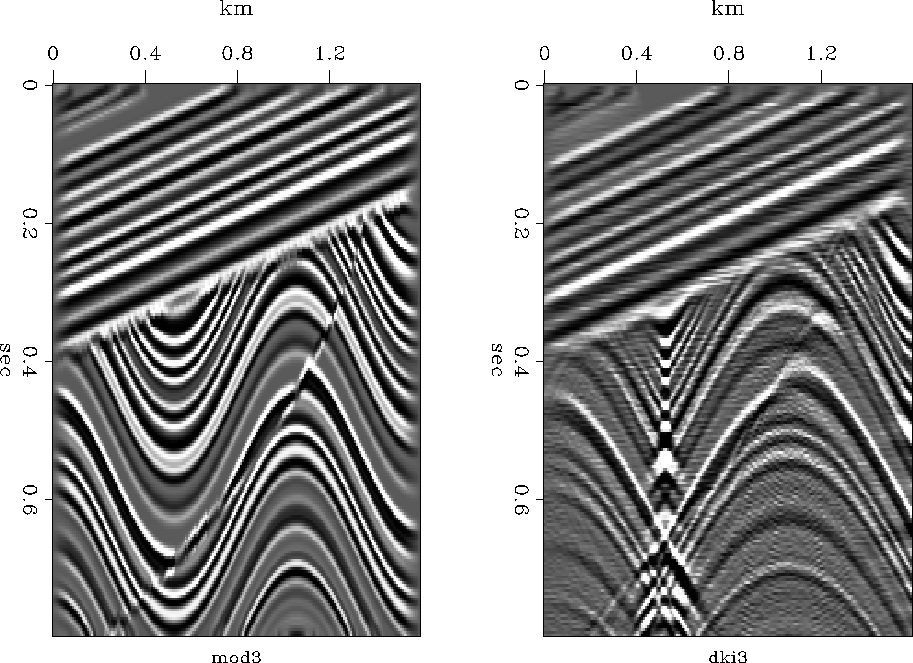
Figure 3 shows an example. The model includes dipping beds, syncline, anticline, fault, unconformity, and buried focus. The result is as expected with a ``bow tie'' at the buried focus. On a video screen, I can see hyperbolic events originating from the unconformity and the fault. At the right edge are a few faint edge artifacts. We could have reduced or eliminated these edge artifacts if we had extended the model to the sides with some empty space.

 

kfgood
Figure 3 Left is the model. Right is diffraction to synthetic data. We notice the ``syncline'' (depression) turns into a ``bow tie'' whereas the anticline (bulge up) broadens.