Next: Tutorial Kirchhoff code
Up: Kirchhoff migration
Previous: THE EXPLODING REFLECTOR CONCEPT
There are two basic tasks to be done:
(1) make data from a model, and (2) make models from data.
The latter is often called imaging.
Imagine the earth had just one point reflector at (x0,z0).
This reflector explodes at t=0.
The data at z=0 is a function of location x and travel time t
would be an impulsive signal along
the hyperbolic trajectory t2 = ((x-x0)2+z02)/v2.
Imagine the earth had more point reflectors in it.
The data would then be a superposition of more hyperbolic arrivals.
A dipping bed could be represented as points along a line in (x,z).
The data from that dipping bed must be
a superposition of many hyperbolic arrivals.
Now let us take the opposite point of view:
we have data and we want to compute a model.
This is called ``migration''.
Conceptually,
the simplest approach to migration is also based on the idea of
an impulse response.
Suppose we recorded data that was zero everywhere
except at one point (x0,t0).
Then the earth model should be a spherical mirror
centered at (x0,z0) because this model produces the required data,
namely, no received signal except when the sender-receiver pair
are in the center of the semicircle.
This observation plus the superposition principle
suggests an algorithm for making earth images:
For each location (x,t) on the data mesh d(x,t) add in
a semicircular mirror of strength d into the model m(x,z).
You need to add in a semicircle for every value of (t,x).
Notice again we use the same equation t2 = (x2+z2)/v2.
This equation is the ``conic section''.
A slice at constant t is a circle in (x,z).
A slice at constant z is a hyperbola in (x,t).
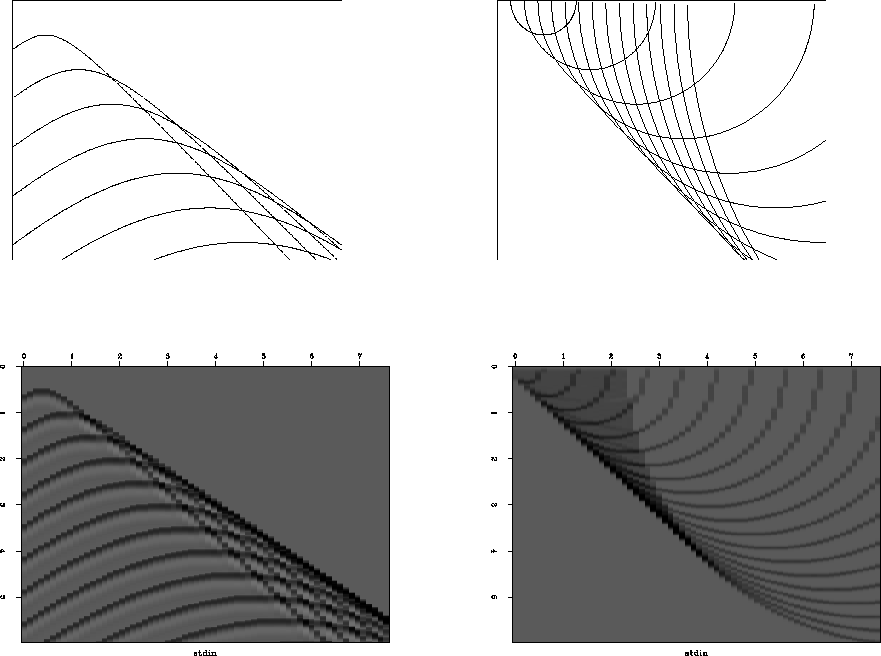
Examples are shown in Figure 2.
Points making up a line reflector diffract to a line reflection, and
how points making up a line reflection migrate to a line reflector.
dip
Figure 2
Left is a superposition of many hyperbolas.
The top of each hyperbola lies along a straight line.
That line is like a reflector, but instead of using a continuous line,
it is a sequence of points.
Constructive interference gives an apparent reflection off to the side.
Right shows a superposition of semicircles.
The bottom of each semicircle lies along a line that
could be the line of an observed plane wave.
Instead the plane wave is broken into point arrivals,
each being interpreted as coming from a semicircular mirror.
Adding the mirrors yields a more steeply dipping reflector.

Besides the semicircle superposition migration method,
there is another migration method
that produces a similar result conceptually,
but it has more desirable results numerically.
This is the ``adjoint modeling'' idea.
In it, we sum the data over a hyperbolic
trajectory to find a value in model space that is located
at the apex of the hyperbola.
This is also called the ``pull'' method of migration.





Next: Tutorial Kirchhoff code
Up: Kirchhoff migration
Previous: THE EXPLODING REFLECTOR CONCEPT
Stanford Exploration Project
3/1/2001