




Next: REFERENCES
Up: THE WORLD OF CONJUGATE
Previous: Standard methods
This section includes Sergey Fomel's explanation on the ``magic''
convergence properties of the conjugate-direction methods. It also
presents a classic version of conjugate gradients, which can be found
in numerous books on least-square optimization.
The key idea for constructing an optimal iteration is to update the
solution at each step in the direction, composed by a linear
combination of the current direction and all previous solution steps.
To see why this is a helpful idea, let us consider first the method of
random directions. Substituting expression (47) into
formula (45), we see that the residual power
decreases at each step by
| 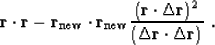 |
(96) |
To achieve a better convergence, we need to maximize the right hand
side of (96). Let us define a new solution step 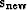 as a combination of the current direction
as a combination of the current direction 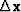 and the previous step
and the previous step  , as follows:
, as follows:
| 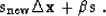 |
(97) |
The solution update is then defined as
| 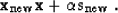 |
(98) |
The formula for  (47) still holds, because we have
preserved in (98) the form of equation (41)
and just replaced
(47) still holds, because we have
preserved in (98) the form of equation (41)
and just replaced 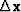 with
with 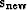 . In fact,
formula (47) can be simplified a little bit. From
(46), we know that
. In fact,
formula (47) can be simplified a little bit. From
(46), we know that 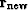 is orthogonal
to
is orthogonal
to 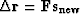 . Likewise,
. Likewise,  should be orthogonal to
should be orthogonal to 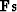 (recall that
(recall that  was
was
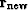 and
and  was
was 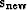 at the
previous iteration). We can conclude that
at the
previous iteration). We can conclude that
| 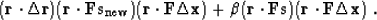 |
(99) |
Comparing (99) with (96), we can see that
adding a portion of the previous step to the current direction does
not change the value of the numerator in expression
(96). However, the value of the denominator can be
changed. Minimizing the denominator maximizes the residual increase at
each step and leads to a faster convergence. This is the denominator
minimization that constrains the value of the adjustable coefficient
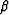 in (97).
in (97).
The procedure for finding 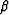 is completely analogous to the
derivation of formula (47). We start with expanding the
dot product
is completely analogous to the
derivation of formula (47). We start with expanding the
dot product 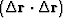 :
:
| 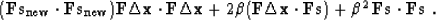 |
(100) |
Differentiating with respect to 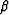 and setting the derivative to
zero,
we find that
and setting the derivative to
zero,
we find that
| 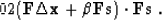 |
(101) |
Equation (101) states that the conjugate direction
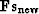 is orthogonal (perpendicular) to the
previous conjugate direction
is orthogonal (perpendicular) to the
previous conjugate direction 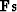 . It also defines the
value of
. It also defines the
value of 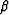 as
as
| 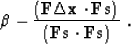 |
(102) |
Can we do even better? The positive quantity that we minimized in
(100) decreased by
| 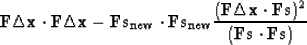 |
(103) |
Can we decrease it further by adding another previous step? In
general, the answer is positive, and it defines the method of
conjugate directions. I will state this result without a formal proof
(which uses the method of mathematical induction).
- If the new step is
composed of the current direction and a combination of all the
previous steps:
| 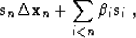 |
(104) |
then the optimal convergence is achieved when
| 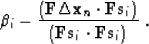 |
(105) |
- The new conjugate direction is orthogonal to the previous ones:
| 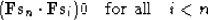 |
(106) |
To see why this is an optimally convergent method, it is sufficient to
notice that vectors 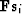 form an orthogonal basis in
the data space. The vector from the current residual to the smallest
residual also belongs to that space. If the data size is n, then n
basis components (at most) are required to represent this vector, hence
no more then n conjugate-direction steps are required to find the
solution.
form an orthogonal basis in
the data space. The vector from the current residual to the smallest
residual also belongs to that space. If the data size is n, then n
basis components (at most) are required to represent this vector, hence
no more then n conjugate-direction steps are required to find the
solution.
The computation template for the method of conjugate directions is
 iterate {
iterate {
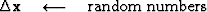
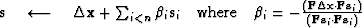
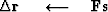
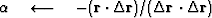

 }
}
What happens if we ``feed'' the method with gradient directions
instead of just random directions? It turns out that in this case we
need to remember from all the previous steps 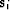 only the one
that immediately precedes the current iteration. Let us derive a
formal proof of that fact as well as some other useful formulas
related to the method of conjugate gradients .
only the one
that immediately precedes the current iteration. Let us derive a
formal proof of that fact as well as some other useful formulas
related to the method of conjugate gradients .
According to formula (46), the new residual 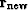 is orthogonal to the conjugate direction
is orthogonal to the conjugate direction 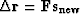 . According to the orthogonality condition
(106), it is also orthogonal to all the previous
conjugate directions. Defining
. According to the orthogonality condition
(106), it is also orthogonal to all the previous
conjugate directions. Defining 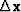 equal to the gradient
equal to the gradient
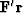 and applying the definition of the adjoint
operator, it is convenient to rewrite the orthogonality condition in
the form
and applying the definition of the adjoint
operator, it is convenient to rewrite the orthogonality condition in
the form
| 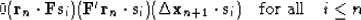 |
(107) |
According to formula (104), each solution step 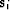 is just a linear combination of the gradient
is just a linear combination of the gradient 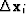 and
the previous solution steps. We deduce from formula
(107) that
and
the previous solution steps. We deduce from formula
(107) that
| 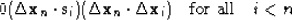 |
(108) |
In other words, in the method of conjugate gradients, the current
gradient direction is always orthogonal to all the previous
directions. The iteration process constructs not only an orthogonal
basis in the data space but also an orthogonal basis in the model
space, composed of the gradient directions.
Now let us take a closer look at formula (105). Note
that 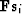 is simply related to the residual step at
i-th iteration:
is simply related to the residual step at
i-th iteration:
| 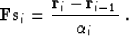 |
(109) |
Substituting relationship (109) into formula
(105) and applying again the definition of the adjoint
operator, we obtain
| 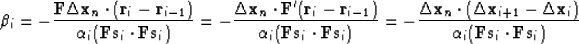 |
(110) |
Since the gradients 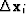 are orthogonal to each other,
the dot product in the numerator is equal to zero unless i = n-1. It
means that only the immediately preceding step
are orthogonal to each other,
the dot product in the numerator is equal to zero unless i = n-1. It
means that only the immediately preceding step 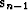 contributes to the definition of the new solution direction
contributes to the definition of the new solution direction 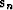 in (104). This is precisely the property of the
conjugate gradient method we wanted to prove.
in (104). This is precisely the property of the
conjugate gradient method we wanted to prove.
To simplify formula (110), rewrite formula (47) as
| 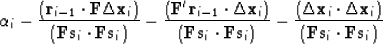 |
(111) |
Substituting (111) into (110), we obtain
| 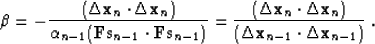 |
(112) |
The computation template for the method of conjugate gradients is then

 iterate {
iterate {
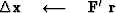 if not the first iteration
if not the first iteration 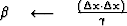
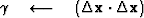

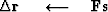
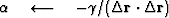

 }
}





Next: REFERENCES
Up: THE WORLD OF CONJUGATE
Previous: Standard methods
Stanford Exploration Project
4/27/2004
![]() is completely analogous to the
derivation of formula (47). We start with expanding the
dot product
is completely analogous to the
derivation of formula (47). We start with expanding the
dot product ![]() :
:
![]() form an orthogonal basis in
the data space. The vector from the current residual to the smallest
residual also belongs to that space. If the data size is n, then n
basis components (at most) are required to represent this vector, hence
no more then n conjugate-direction steps are required to find the
solution.
form an orthogonal basis in
the data space. The vector from the current residual to the smallest
residual also belongs to that space. If the data size is n, then n
basis components (at most) are required to represent this vector, hence
no more then n conjugate-direction steps are required to find the
solution.
iterate {
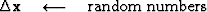
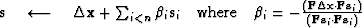
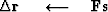
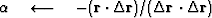

}
![]() only the one
that immediately precedes the current iteration. Let us derive a
formal proof of that fact as well as some other useful formulas
related to the method of conjugate gradients .
only the one
that immediately precedes the current iteration. Let us derive a
formal proof of that fact as well as some other useful formulas
related to the method of conjugate gradients .
![]() is orthogonal to the conjugate direction
is orthogonal to the conjugate direction ![]() . According to the orthogonality condition
(106), it is also orthogonal to all the previous
conjugate directions. Defining
. According to the orthogonality condition
(106), it is also orthogonal to all the previous
conjugate directions. Defining ![]() equal to the gradient
equal to the gradient
![]() and applying the definition of the adjoint
operator, it is convenient to rewrite the orthogonality condition in
the form
and applying the definition of the adjoint
operator, it is convenient to rewrite the orthogonality condition in
the form
![]() is simply related to the residual step at
i-th iteration:
is simply related to the residual step at
i-th iteration:

iterate {
if not the first iteration
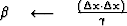
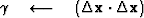

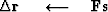
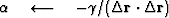

}