




Next: Null space and iterative
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Sign convention
random directions steepest descent
Let us minimize the sum of the squares of the components
of the residual vector given by
| ![\begin{eqnarray}
{\rm residual}
&=&
{\rm
\quad \hbox{transform} \quad \quad \hb...
...array}
{c}
\\ \\ \\ \bold d \\ \\ \\ \
\end{array}\right]\end{eqnarray}](img100.gif) |
(39) |
| (40) |
A contour plot is based on an altitude function of space.
The altitude is the dot product 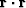 .By finding the lowest altitude,
we are driving the residual vector
.By finding the lowest altitude,
we are driving the residual vector  as close as we can to zero.
If the residual vector
as close as we can to zero.
If the residual vector  reaches zero, then we have solved
the simultaneous equations
reaches zero, then we have solved
the simultaneous equations 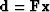 .In a two-dimensional world the vector
.In a two-dimensional world the vector  has two components,
(x1 , x2 ).
A contour is a curve of constant
has two components,
(x1 , x2 ).
A contour is a curve of constant
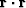 in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), with measurement errors in
in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), with measurement errors in 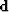 .
.
Let us see how a random search-direction
can be used to reduce the residual
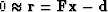 .Let
.Let 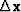 be an abstract vector
with the same number of components as the solution
be an abstract vector
with the same number of components as the solution  ,and let
,and let 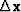 contain arbitrary or random numbers.
We add an unknown quantity
contain arbitrary or random numbers.
We add an unknown quantity  of vector
of vector 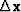 to the vector
to the vector  ,and thereby create
,and thereby create 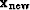 :
:
| 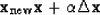 |
(41) |
This gives a new residual:
| 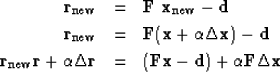 |
(42) |
| (43) |
| (44) |
which defines 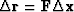 .
.
Next we adjust  to minimize the dot product:
to minimize the dot product:
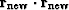
| 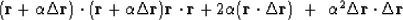 |
(45) |
Set to zero its derivative with respect to  using the chain rule
using the chain rule
| 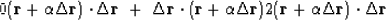 |
(46) |
which says that
the new residual 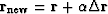 is
perpendicular to the ``fitting function''
is
perpendicular to the ``fitting function'' 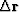 .Solving gives the required value of
.Solving gives the required value of  .
.
| 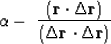 |
(47) |
A ``computation template'' for the method of random directions is
 iterate {
iterate {
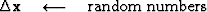
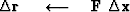
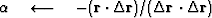

 }
}
A nice thing about the method of random directions is that you
do not need to know the adjoint operator 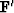 .
.
In practice, random directions are rarely used.
It is more common to use the gradient direction than a random direction.
Notice that a vector of the size of 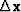 is
is
| 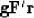 |
(48) |
Notice also that this vector can be found by taking the gradient
of the size of the residuals:
| 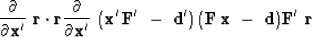 |
(49) |
Choosing 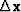 to be the gradient vector
to be the gradient vector
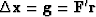 is called ``the method of steepest descent.''
is called ``the method of steepest descent.''
Starting from a model 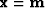 (which may be zero),
below is a template of pseudocode for minimizing the residual
(which may be zero),
below is a template of pseudocode for minimizing the residual
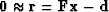 by the steepest-descent method:
by the steepest-descent method:
 iterate {
iterate {
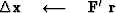
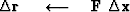
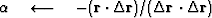

 }
}





Next: Null space and iterative
Up: KRYLOV SUBSPACE ITERATIVE METHODS
Previous: Sign convention
Stanford Exploration Project
4/27/2004
![\begin{eqnarray}
{\rm residual}
&=&
{\rm
\quad \hbox{transform} \quad \quad \hb...
...array}
{c}
\\ \\ \\ \bold d \\ \\ \\ \
\end{array}\right]\end{eqnarray}](img100.gif)
![\begin{eqnarray}
{\rm residual}
&=&
{\rm
\quad \hbox{transform} \quad \quad \hb...
...array}
{c}
\\ \\ \\ \bold d \\ \\ \\ \
\end{array}\right]\end{eqnarray}](img100.gif)
![]() .By finding the lowest altitude,
we are driving the residual vector
.By finding the lowest altitude,
we are driving the residual vector ![]() as close as we can to zero.
If the residual vector
as close as we can to zero.
If the residual vector ![]() reaches zero, then we have solved
the simultaneous equations
reaches zero, then we have solved
the simultaneous equations ![]() .In a two-dimensional world the vector
.In a two-dimensional world the vector ![]() has two components,
(x1 , x2 ).
A contour is a curve of constant
has two components,
(x1 , x2 ).
A contour is a curve of constant
![]() in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), with measurement errors in
in (x1 , x2 )-space.
These contours have a statistical interpretation as contours
of uncertainty in (x1 , x2 ), with measurement errors in ![]() .
.![]() .Let
.Let ![]() be an abstract vector
with the same number of components as the solution
be an abstract vector
with the same number of components as the solution ![]() ,and let
,and let ![]() contain arbitrary or random numbers.
We add an unknown quantity
contain arbitrary or random numbers.
We add an unknown quantity ![]() of vector
of vector ![]() to the vector
to the vector ![]() ,and thereby create
,and thereby create ![]() :
:
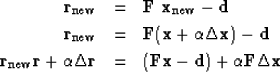
![]() to minimize the dot product:
to minimize the dot product:
![]()
iterate {
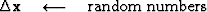
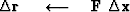
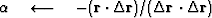

}
![]() is
is
![]() (which may be zero),
below is a template of pseudocode for minimizing the residual
(which may be zero),
below is a template of pseudocode for minimizing the residual
![]() by the steepest-descent method:
by the steepest-descent method:
iterate {
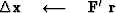
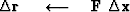
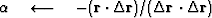

}