 |
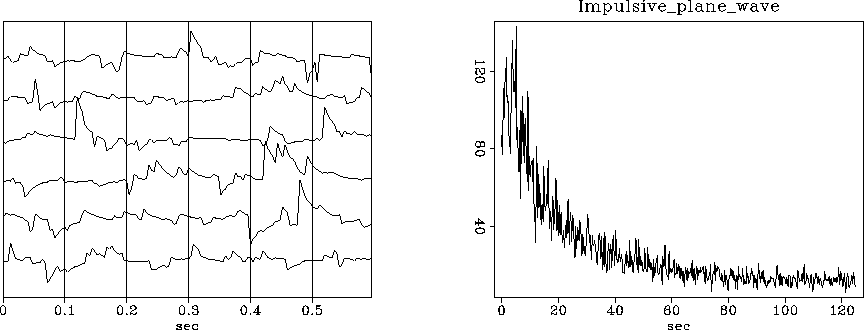
Figure 5 Left is sparse random noise passed through a leaky integrator. Right is the amplitude spectrum of the output.
 |
The output spectral amplitude of an integrator should be ![]() ,but the decay constant in the leaky integrator gives instead the amplitude
,but the decay constant in the leaky integrator gives instead the amplitude
![]() .Since the random numbers are sparse,
you can see damped exponents in the data itself.
This enables us to confirm the direction of the time axis.
If the random numbers had been Gaussian,
the spectrum would be the same,
but we would be able neither to see
the damped exponents nor detect the direction of time.
.Since the random numbers are sparse,
you can see damped exponents in the data itself.
This enables us to confirm the direction of the time axis.
If the random numbers had been Gaussian,
the spectrum would be the same,
but we would be able neither to see
the damped exponents nor detect the direction of time.