| (8) |
| (9) |
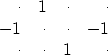 |
(10) |
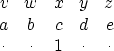 |
(11) |
Let us examine the Fourier domain for this filter. The filter (10) was transformed to the Fourier domain; it was multiplied by its conjugate; the square root was taken; and contours are plotted at near-zero magnitudes in Figure 18. The slanting straight lines have slopes at the two dips that are destroyed by the filters. Noticing the broad lows where the null lines cross, we might expect to see energy at this temporal and spatial frequency, but I have not noticed any.
|
fk2dip
Figure 18 Magnitude of two-dimensional Fourier transform of the 2-D filter contoured at .01 and at .1. | 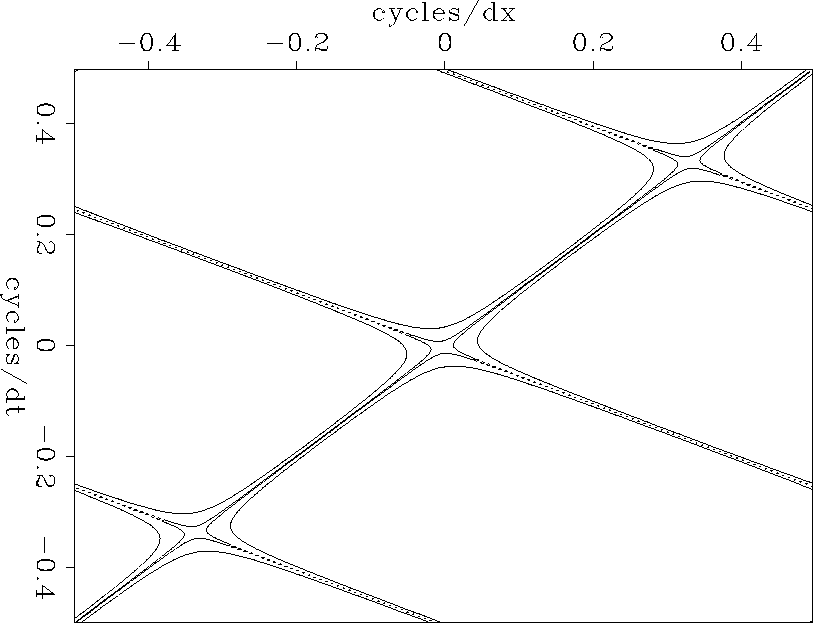 |
# CINJOF -- Convolution INternal with Jumps. Output and FILTER are adjoint.
#
subroutine cinjof( adj, add, jump, n1,n2,xx, nb1,nb2,bb, yy)
integer adj, add, jump, n1,n2, nb1,nb2 # jump subsamples data
real xx( n1,n2), bb( nb1,nb2), yy( n1,n2)
integer y1,y2, x1,x2, b1, b2, ny1, ny2
call adjnull( adj, add, bb, nb1*nb2, yy, n1*n2)
ny1 = n1 - (nb1-1) * jump; if( ny1<1 ) call erexit('cinjof: ny1<1')
ny2 = n2 - (nb2-1); if( ny2<1 ) call erexit('cinjof: ny2<1')
if( adj == 0 )
do b2=1,nb2 { do y2=1,ny2 { x2 = y2 - (b2-nb2)
do b1=1,nb1 { do y1=1,ny1 { x1 = y1 - (b1-nb1) * jump
yy(y1,y2) = yy(y1,y2) + bb(b1,b2) * xx(x1,x2)
}} }}
else
do b2=1,nb2 { do y2=1,ny2 { x2 = y2 - (b2-nb2)
do b1=1,nb1 { do y1=1,ny1 { x1 = y1 - (b1-nb1) * jump
bb(b1,b2) = bb(b1,b2) + yy(y1,y2) * xx(x1,x2)
}} }}
return; end
In practice, wavefronts have curvature,
so we will estimate the 2-D filters
in many small windows on a wall of data.
Therefore, to eliminate edge effects, I designed the 2-D filter programs
starting from the 1-D internal convolution program
convin() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The subroutine for two-dimensional filtering is
cinjof()
.
The subroutine for two-dimensional filtering is
cinjof() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The adjoint operation included in this subroutine is exactly
what we need for estimating the filter.
.
The adjoint operation included in this subroutine is exactly
what we need for estimating the filter.
A companion program, cinloi(), is essentially the same as cinjof(), except that in cinloi() the other adjoint is used (for unknown input instead of unknown filter), and there is no need to interlace the time axis. A new feature of cinloi() is that it arranges for the output residuals to come out directly on top of their appropriate location on the original data. In other words, the output of the filter is at the ``1.'' Although the edge conditions in this routine are confusing, it should be obvious that xx(,) is aligned with yy(,) at bb(lag1,lag2).
# CINLOI -- Convolution INternal with Lags. Output is adjoint to INPUT.
#
subroutine cinloi( adj, add, lag1,lag2,nb1,nb2,bb, n1,n2, xx, yy)
integer adj, add, lag1,lag2,nb1,nb2, n1,n2 # lag=1 causal
real bb(nb1,nb2), xx(n1,n2), yy(n1,n2)
integer y1,y2, x1,x2, b1,b2
call adjnull( adj, add, xx,n1*n2, yy,n1*n2 )
if( adj == 0 )
do b2=1,nb2 { do y2= 1+nb2-lag2, n2-lag2+1 { x2= y2 - b2 + lag2
do b1=1,nb1 { do y1= 1+nb1-lag1, n1-lag1+1 { x1= y1 - b1 + lag1
yy(y1,y2) = yy(y1,y2) + bb(b1,b2) * xx(x1,x2)
}} }}
else
do b2=1,nb2 { do y2= 1+nb2-lag2, n2-lag2+1 { x2= y2 - b2 + lag2
do b1=1,nb1 { do y1= 1+nb1-lag1, n1-lag1+1 { x1= y1 - b1 + lag1
xx(x1,x2) = xx(x1,x2) + bb(b1,b2) * yy(y1,y2)
}} }}
return; end