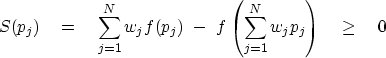Next: Examples of Jensen inequalities
Up: Entropy and Jensen inequality
Previous: Entropy and Jensen inequality
Let f be a function with a positive second derivative.
Such a function is called
``convex" and satisfies the inequality
| 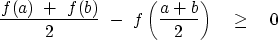 |
(1) |
Equation (1) relates a function of an average to
an average of the function.
The average can be weighted, for example,
| 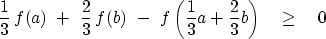 |
(2) |
Figure 1 is a graphical interpretation
of equation (2)
for the function f=x2.
jen
Figure 1
Sketch of y=x2 for interpreting
equation ((2)).
|
| 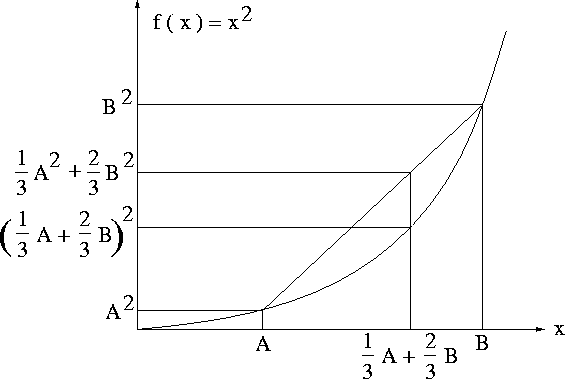 |

There is nothing special about f=x2,
except that it is convex.
Given three numbers a, b, and c,
the inequality (2) can first be applied to a and b,
and then to c and the average of a and b.
Thus, recursively,
an inequality like (2)
can be built for a weighted average of three or more numbers.
Define weights 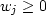 that are normalized
(
that are normalized
(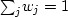 ).
The general result is
).
The general result is
| 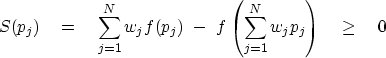 |
(3) |
If all the pj are the same,
then both of the two terms in S are the same,
and S vanishes.
Hence, minimizing S is like urging all the pj to be identical.
Equilibrium is when S is reduced
to the smallest possible value
which satisfies any constraints that may be applicable.
The function S defined by (3)
is like the
entropy
defined in
thermodynamics.





Next: Examples of Jensen inequalities
Up: Entropy and Jensen inequality
Previous: Entropy and Jensen inequality
Stanford Exploration Project
10/21/1998
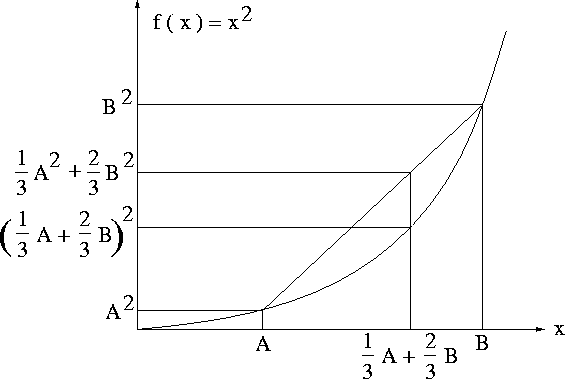
![]() that are normalized
(
that are normalized
(![]() ).
The general result is
).
The general result is