Completing the physical derivation of the dispersion relation,
| |
(29) |
|
evtheory
Figure 15 The triangle(s) of reflection energy | 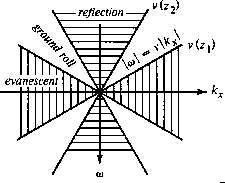 |
When ![]() exceeds
exceeds ![]() , the familiar downward-extrapolation
expression is better rewritten as
, the familiar downward-extrapolation
expression is better rewritten as
| |
(30) |
Perhaps a better physical description is
a thought experiment with a
sinusoidally corrugated sheet.
Such metallic sheet is sometimes used for roofs or garage doorways.
The wavelength of the corrugation fixes kx.
Moving such a sheet past your ear at
velocity V you would hear a frequency of
oscillation equal to ![]() , regardless of whether V is
larger or smaller than the speed of sound in air.
But the sound you hear would get weaker exponentially with distance from
the sheet unless it moved very fast, V > v, in which case
the moving sheet would be radiating sound to great distances.
This is why supersonic airplanes use so much fuel.
, regardless of whether V is
larger or smaller than the speed of sound in air.
But the sound you hear would get weaker exponentially with distance from
the sheet unless it moved very fast, V > v, in which case
the moving sheet would be radiating sound to great distances.
This is why supersonic airplanes use so much fuel.
What should a migration program do with energy that moves
slower than the sound speed?
Theoretically, such energy should be exponentially damped in the direction
going away from the source.
The damping in
the offending region of ![]() -space
is, quantitatively, extremely rapid.
Thus, simple exploding-reflector theory predicts that there should be
almost no energy in the data at these low velocities.
-space
is, quantitatively, extremely rapid.
Thus, simple exploding-reflector theory predicts that there should be
almost no energy in the data at these low velocities.
The reality is that,
instead of tiny amounts of energy in the evanescent region
of ![]() -space, there is often a great deal.
This is another breakdown of the exploding-reflector concept.
The problem is worst with land data.
Waves that are evanescent in deep, fast rocks of interest
can be propagating in the low-velocity soil layer.
This energy is called
ground roll.
Figure 16 shows an example.
-space, there is often a great deal.
This is another breakdown of the exploding-reflector concept.
The problem is worst with land data.
Waves that are evanescent in deep, fast rocks of interest
can be propagating in the low-velocity soil layer.
This energy is called
ground roll.
Figure 16 shows an example.
|
evdata
Figure 16 Florida shallow marine profile, exhibiting ground roll with frequency dispersion. (Conoco, Yedlin) |  |
This data is not a zero-offset section. The shot is on the left, and the traces to the right are from geophones at increasing distances from the shot. First draw a line on the figure going through origin and at a slope of the water velocity, 1.5 km/sec. Steeper slopes are slower surface waves. Geological events have lesser slopes. Like the surface of the earth, which varies greatly from place to place, the immediate subsurface which controls the ground roll varies substantially. So although Figure 16 is a nice example, no example can really be typical. In this figure there are two types of ground roll, one at about half of water velocity, and a stronger one at about a quarter of water velocity. The later and stronger one shows an interesting feature known as frequency dispersion. Viewing the data from the side, you should be able to notice that the high frequencies arrive before the low frequencies.
Ground roll is unwanted noise since its exponential decay effectively prevents
it from being influenced by deep objects of interest.
In practice, energy in the offending region of ![]() -space
should be attenuated.
A mathematical description is to say that the composite mapping from
model space to data space and back to model space again is
not an identity transformation but an idempotent transformation.
-space
should be attenuated.
A mathematical description is to say that the composite mapping from
model space to data space and back to model space again is
not an identity transformation but an idempotent transformation.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) use a negative sign on kz
whereas phasemod()
use a negative sign on kz
whereas phasemod() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) uses a positive sign
even though both
are dealing with upcoming waves?
uses a positive sign
even though both
are dealing with upcoming waves?