The phase-shift method proceeds straightforwardly by extrapolating
downward with ![]() and subsequently evaluating the
wavefield at t = 0 (the reflectors explode at t=0).
Of all the wide-angle methods it most easily incorporates depth variation in
velocity.
Even the phase angle and obliquity function are correctly included,
automatically.
Unlike Kirchhoff methods, with this method
there is no danger of aliasing the operator.
and subsequently evaluating the
wavefield at t = 0 (the reflectors explode at t=0).
Of all the wide-angle methods it most easily incorporates depth variation in
velocity.
Even the phase angle and obliquity function are correctly included,
automatically.
Unlike Kirchhoff methods, with this method
there is no danger of aliasing the operator.
The phase-shift method begins with a two-dimensional Fourier transform (2D-FT)
of the dataset.
Then the transformed data values, all in the ![]() -plane,
are downward continued to
a depth
-plane,
are downward continued to
a depth ![]() by multiplying by
by multiplying by
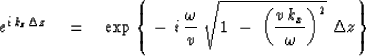 |
(20) |
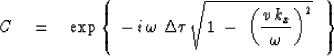 |
(21) |
Next is the task of imaging.
At each depth an inverse Fourier transform is followed
by selection of its value at t = 0.
(Reflectors explode at t=0).
Luckily, only the Fourier transform at one point, t = 0, is needed, so
that is all that need be computed.
The computation is especially easy since the value at t = 0 is merely a
summation of each ![]() frequency component. (This may be seen
by substituting t=0 into the inverse Fourier integral). Finally,
inverse Fourier transform kx to x.
The migration process,
computing the image from the upcoming wave u,
may be summarized in the following pseudo code:
frequency component. (This may be seen
by substituting t=0 into the inverse Fourier integral). Finally,
inverse Fourier transform kx to x.
The migration process,
computing the image from the upcoming wave u,
may be summarized in the following pseudo code:
![\begin{displaymath}
\vbox{
\begin{tabbing}
$U(\omega, k_x, \tau = 0) = FT[u(t, ...
... gt image$(x, \tau) = FT[$Image$(k_x, \tau)]$ \\ \end{tabbing}}\end{displaymath}](img59.gif)
This pseudo code Fourier transforms a wavefield
observed at the earth's surface ![]() ,and then it marches that wavefield down into the earth (
,and then it marches that wavefield down into the earth (![]() )filling up a three-dimensional function,
)filling up a three-dimensional function, ![]() .Then it selects t=0, the time of the exploding reflectors
by summing over all frequencies
.Then it selects t=0, the time of the exploding reflectors
by summing over all frequencies ![]() .(Mathematically,
this resembles finding the signal at
.(Mathematically,
this resembles finding the signal at ![]() by summing over all t).
by summing over all t).
Turning from pseudocode to real code,
an important practical reality
is that computer memories are not big enough
for the three-dimensional function ![]() .But it is easy to intertwine the downward continuation
with the summation over
.But it is easy to intertwine the downward continuation
with the summation over ![]() so a three-dimensional function need not be kept in memory.
This is done in the real code in subroutine phasemig().
so a three-dimensional function need not be kept in memory.
This is done in the real code in subroutine phasemig().
subroutine phasemig( u, nt, nx, dt, dx, image, ntau, dtau, v)
integer nt,nw,nx,ntau, iw,ikx,itau
real dt,dx, w,w0,dw, kx,kx0,dkx,dtau, kzkz, v, sig1,sig2,pi, signum
complex u(nt,nx), image(ntau,nx), c
pi = 3.14159265; sig1 =+1.; sig2 =-1.
call ft1axis( 0, sig1, nt, nx, u)
call ft2axis( 0, sig2, nt, nx, u)
w0 = -pi/dt; dw = 2.*pi/(nt*dt); nw = nt
kx0 = -pi/dx; dkx= 2.*pi/(nx*dx)
call zero( ntau*nx, image)
do itau = 1, ntau {
do ikx = 2, nx { kx = kx0 + (ikx-1) * dkx
do iw = 2, nw { w = w0 + (iw-1) * dw
kzkz = w*w - v*v * kx*kx
if (kzkz >0) { c = cexp(cmplx(0., -signum(w)*dtau*sqrt(kzkz))) }
else { c = 0. }
u(iw,ikx) = u(iw,ikx) * c
image(itau,ikx) = image(itau,ikx) + u(iw,ikx)
}}}
call ft2axis( 1, sig2, ntau, nx, image)
return; end
An aspect of the computation that was hidden in the pseudo code
that you can see in the real code
is that we must also handle negative frequencies.
When doing so, we use the signum function
![]() to choose the sign of kz
so that the sign of kz is always opposite that of
to choose the sign of kz
so that the sign of kz is always opposite that of ![]() .
.
Inverse migration (modeling) proceeds in much the same way.
Beginning from an upcoming wave that is zero at great depth,
the wave is marched upward in steps
by multiplication with ![]() .As each level in the earth is passed,
exploding reflectors from that level are added into the upcoming wave.
Pseudo code for modeling the upcoming wave u is
.As each level in the earth is passed,
exploding reflectors from that level are added into the upcoming wave.
Pseudo code for modeling the upcoming wave u is
![\begin{displaymath}
\vbox{
\begin{tabbing}
Image$(k_x, z) = FT[$image$(x, z)]$ \...
...gt \} \} \} \\ $u(t, x) = FT[U(\omega, k_x)]$ \\ \end{tabbing}}\end{displaymath}](img66.gif)
Some real code for this job is in subroutine phasemod().
subroutine phasemod( image, nz, nx, dz, dx, u, nt, dt, v)
integer nt,nw,nx,nz, iw,ikx,iz
real dt,dx,dz, w,w0,dw, kx,kx0,dkx, kzkz, v, sig1,sig2,pi, signum
complex u(nt,nx), image(nz,nx), c
pi = 3.14159265; sig1=+1.; sig2=-1.
call ft2axis( 0, sig2, nz, nx, image)
w0 = -pi/dt; dw = 2.*pi/(nt*dt); nw = nt
kx0 = -pi/dx; dkx= 2.*pi/(nx*dx)
call zero( nw*nx, u)
do iw = 2, nw { w = w0 + (iw-1) * dw
do ikx = 2, nx { kx = kx0 + (ikx-1) * dkx
do iz = nz, 1, -1 {
kzkz = w*w - (v*v) * kx*kx
if (kzkz >0) { c = cexp(cmplx(0., signum(w)*dz*sqrt(kzkz))) }
else { c = 0. }
u(iw,ikx) = u(iw,ikx) * c
u(iw,ikx) = u(iw,ikx) + image(iz,ikx)
}}}
call ft1axis( 1, sig1, nt, nx, u)
call ft2axis( 1, sig2, nt, nx, u)
return; end
The positive sign in the complex exponential is a combination of two negatives,
the up
coming wave and the upward extrapolation.
The three loops on ![]() , kx, and z are interchangeable.
When the velocity v is a constant function of depth the program
can be speeded by moving the computation
of the complex exponential C out of the inner loop on z.
, kx, and z are interchangeable.
When the velocity v is a constant function of depth the program
can be speeded by moving the computation
of the complex exponential C out of the inner loop on z.