Absorption

A basic model arises when ${v ( \omega ) }$ is defined by the equation  

$${-i \omega \over v ( \omega ) } \eq {\omega_0 \over v_0} \ \left( {-i \omega \over \omega_0} \ \right)^{ 1 - \epsilon }$$ (4)

For $\epsilon=0$, equation (4) gives a constant velocity. Equation (4) models the so-called causal, constant Q attenuation where $Q^{-1} = \tan \, \pi \epsilon$.Figure 3 shows an example of a synthetic seismogram generated by the exploding-reflector model using equations (2), (3) and (4).

 

qhale
Figure 3 Synthetic seismogram for an earth with $Q\ \approx\ 100$. (Hale)

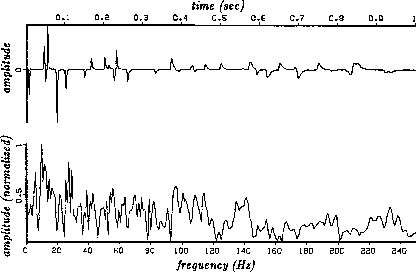Equation (4) creates attenuation by introducing an imaginary part into the velocity. The main effect of this attenuation is to weaken the arrivals at late time. A secondary effect is to make the frequency content of late arrivals lower. A tertiary effect is this: It happens that the requirement of causality forces the real part of the velocity to be slightly frequency-dependent. In the figure, this slight frequency-dependence is evidenced by the ``rise time'' on each pulse being faster than the ``fall time.'' This means that the high frequencies are traveling slightly faster than the low frequencies. In practice, this tertiary effect is rarely noticeable.

In making earth images, earth dissipation might be compensated by amplifying high-frequency energy during downward continuation. This might be done just like migration, except that $k_z = -\sqrt{ \omega^2 / v^2 - k_x^2 }$ would be replaced by something like $ik_z = (-i \omega )^{{1-} \epsilon}$.In practice, however, no one would really do this, since it would amplify high frequency noise. This raises the issue of signal-to-noise ratio.

Noise isn't simply an ambient random fluctuation. It is mainly repeatable if the data is reshot. Noise is anything for which we have no satisfactory model. On a practical level, time-variable filters are often used to select pleasing time-variable passbands. Equations (2), (3) and (4) could be used for this implementation of time-variable filters, but it would be an oversimplification to view their use as compensation for the earth Q.