Dispersion

The frequency-dependence of velocity in the case of surface waves is more dramatic. For example, a frequency-dependent velocity is given by the equation  

$${-i \omega \over v ( \omega ) } \eq {-i \omega \over v_0} \ \sqrt{1\ +\ \omega_0^2 / \omega^2 }$$ (5)

The left side of Figure 4 contains some frequency-dispersive ground roll. On the right side of Figure 4, the dispersion has been backed out by a migration-like process. One difference between this process and migration is that migration extrapolates down the z-axis whereas on the right of Figure 4 the extrapolation is along the x-axis. (The extrapolation direction is really just in the computer).

 

sword
Figure 4 Dispersive surface wave (left), with the frequency dispersion backed out (right). Bottom shows two arrivals, the direct, straight-line arrival, and a hyperbola flank. The hyperbola represents sidescatter that must come from some object on the earth's surface off to the side of the survey line. (Conoco, Sword)

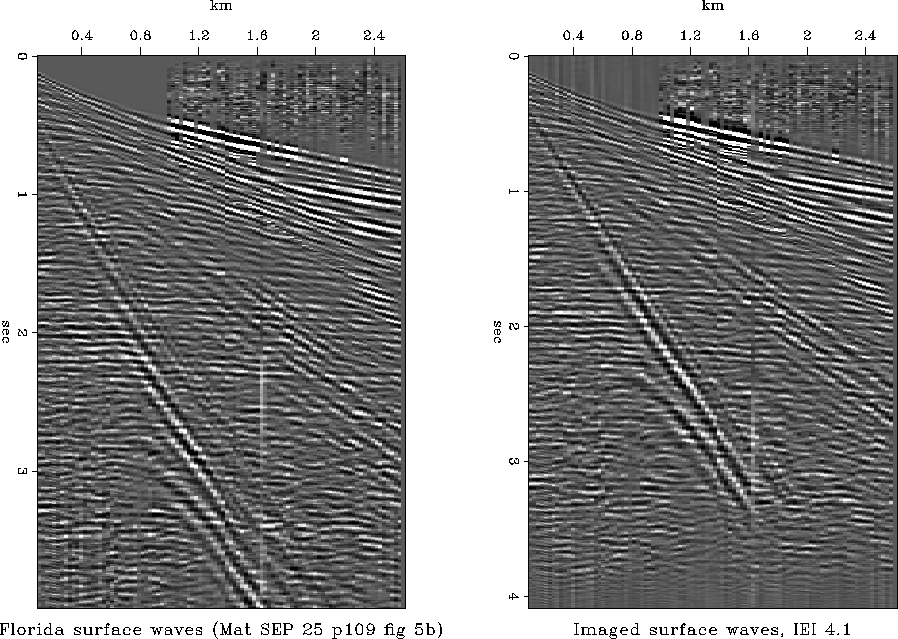Each trace on the right of Figure 4 is processed separately. In migration, data p(t,z=0) is extrapolated to an image p(t=0,z) using a dispersion relation $k_z = -\sqrt{ \omega^2 / v^2 - k_x^2 }$.In this process, data p(t,x=0) is extrapolated to an image p(t=0,x) using a dispersion relation like $k_x = f( \omega /v )$.After this pseudomigration a pseudodiffraction is done with a constant velocity. The total effect is to undo the frequency dispersion. Finally, it is possible to see that the noise consists of two separate events. Techniques resembling this one were first used to locate faults in coal seams (Beresford-Smith and Mason [1980]).