Program

Many of the figures in the book were made with the program presented here. To enable you to reproduce them I am including the complete program. The parameter input and data output calls are site dependent, but I include them anyway to help clarify the defaults, increasing the odds that you can get exactly what I did.  

# representations of   e^{-sqrt{ (-i omega /v)^2 + k^2 } z}
#
subroutine allhyp()
integer fetch
integer iw,nw,ik,nk, omhat, kxhat, kzhat, degree, tfilt, xfilt 
real v, dt, dx, dz, xf, x0, tf, tau0,  rho, bi, r0, eps,  pi, omega, k, vk2
complex cz, cs, cikz, cexp, cmplx, csqrt, cp(1024)
                call putch('esize','i', 8)      # complex numbers
nw = 256;       call putch(   'n1','i',nw)      # inner index is omega
nk = 64;        call putch(   'n2','i',nk)      # outer index is k_x
                call putch(   'n3','i', 1)      # one frame movie

if( fetch(     'v', 'f',     v) == 0 )  v    = 3.754    # rock vel
if( fetch(    'dt', 'f',    dt) == 0 )  dt   = .004     # Delta t, sec
if( fetch(    'dx', 'f',    dx) == 0 )  dx   = .025     # Delta x, km
if( fetch(    'dz', 'f',    dz) == 0 )  dz   = .004     # Delta z, sec
if( fetch(    'xf', 'f',    xf) == 0 )  xf   = .25;   x0  =xf*nk*dx
if( fetch(    'tf', 'f',    tf) == 0 )  tf   = .5;    tau0=tf*nw*dt

if( fetch( 'omhat', 'i', omhat)==0)     omhat = 0       # omega HAT
if( fetch( 'kxhat', 'i', kxhat) == 0 )  kxhat = 0       # {k HAT}_x
if( fetch( 'kzhat', 'i', kzhat) == 0 )  kzhat = 0       # {k HAT}_z
if( fetch('degree', 'i',degree) == 0 )  degree= 90
if( fetch( 'tfilt', 'i', tfilt) == 0 )  tfilt = 1
if( fetch( 'xfilt', 'i', xfilt) == 0 )  xfilt = 1

if( fetch(   'rho', 'f',   rho) == 0 )  rho   = 1-4./nw
if( fetch(    'bi', 'f',    bi) == 0 )  bi    = 6.726   # b^{-1}
if( fetch(    'r0', 'f',    r0) == 0 )  r0    = 0.7071
if( fetch(   'eps', 'f',   eps) == 0 )  eps   = 0.

call putch('d1','f', dt);       call putch('label1','s','sec')
call putch('d2','f', dx);       call putch('label2','s','kilometers')

call hclose()                   # close data description file
pi = 3.14159265

do ik= 1, nk {                  # loop over all k_x
        k = 2*pi * (ik-1.) / nk
        if( k > pi )    k = k - 2*pi
        k = k / dx
        if( kxhat == 0 )
                vk2 = (v/2)**2 * k*k
        else
                vk2 = (v/2)**2 * (2/dx)**2 * sin(k*dx/2)**2  / (1 -
                                      (4./bi) * sin(k*dx/2)**2 )

do iw= 1, nw {                  # loop over all omega
                omega = 2*pi * (iw-1.) / nw
                if( omega > pi )        omega = omega - 2*pi
                omega = omega / dt
                cz = cexp( cmplx( 0., omega * dt ) )
                if( omhat == 0 )        
                        cs = cmplx( 1.e-5 / dt, - omega)
                else
                        cs = (2./dt) * (1. - rho * cz) / (1. + rho * cz)
                if ( degree == 90 )
                        cikz = vk2 / ( csqrt( cs * cs + vk2 ) + cs )
                if ( degree == 15  ||  degree == 45 )
                        cikz = vk2 / ( eps + (r0+1.) * cs )
                if (degree == 45 )
                        cikz =  vk2 / ( 2.*cs + cikz)
                if( real( cikz) < 0.) call erexit('cikz not positive real')

if( kzhat == 0 )
                        cp(iw)= cexp( - tau0  * cikz )
                else
                        cp(iw)= ((1.-cikz * dz/2) /(1.+cikz * dz/2)) **(tau0/dz)
                cp(iw) = cp(iw) * cexp(cmplx(0., omega * tau0 ))   # unretard

if( tfilt >= 1 ) cp(iw) = cp(iw) * (1+cz) / (1 - .8 * cz)
                if( tfilt >= 2 ) cp(iw) = cp(iw) * (1-cz) / (1 - .8 * cz)
                if( xfilt == 1 ) cp(iw) = cp(iw) * (1+cos(k*dx)) / (1+.85*cos(k*dx))
                cp(iw) = cp(iw) * cexp( cmplx(0.,k*x0) )        
                }
        call srite( 'out', cp, 8*nw )   # write
        }
call exit(0);   end

Twenty-two plots displayed in this book were made with this program. The output of the program is 2-D Fourier transformed, the real part taken, and plotted. Different input parameters for the different plots are in the table below.

Figure Default parameter overrides

a tfilt=0 b a

$$\hat \omega$$ b

$$\hat \omega v\,=\,2.0$$ 1a

$$\hat \omega v\,=\,2.0$$ 1b

$$^\circ$$ 5a

$$^\circ \epsilon\,=\,1$$ 5b

$$^\circ$$ 6a

$$^\circ \epsilon\,=\,1$$ 6b

$$^\circ \hat \omega$$ 16

$$^\circ$$ 20a

$$^\circ \hat \omega {\hat k}_x \hat k_z$$ 20b

$${\hat k}_x \hat \omega$$ 22a

$${\hat k}_x \hat \omega$$ 22b

$${\hat k}_x \hat \omega$$ 22c

$${\hat k}_x \hat \omega$$ 22d

$${\hat k}_x \hat \omega$$ 22e a

$$\hat \omega$$ b

$$\Delta z ^\circ \hat \omega {\hat k}_x \hat k_z$$ 23a

$$\Delta z ^\circ \hat \omega {\hat k}_x \hat k_z$$ 23b

It is rumored that accuracy can be improved by making the z mesh coarser. This couldn't happen if x and t were in the continuum, but since they may be discretized, there is the possibility of errors fortuitously canceling. To test this rumor, I tried tripling $\Delta z$ (actually, tripling the increment in travel-time depth). The result is in Figure 23.

 

bigdz
Figure 23 Left is a 45$^\circ$ point diffraction in (x,z,t)-space with $\Delta z =v\Delta t$. At the right, with $\Delta z =3v\Delta t$.

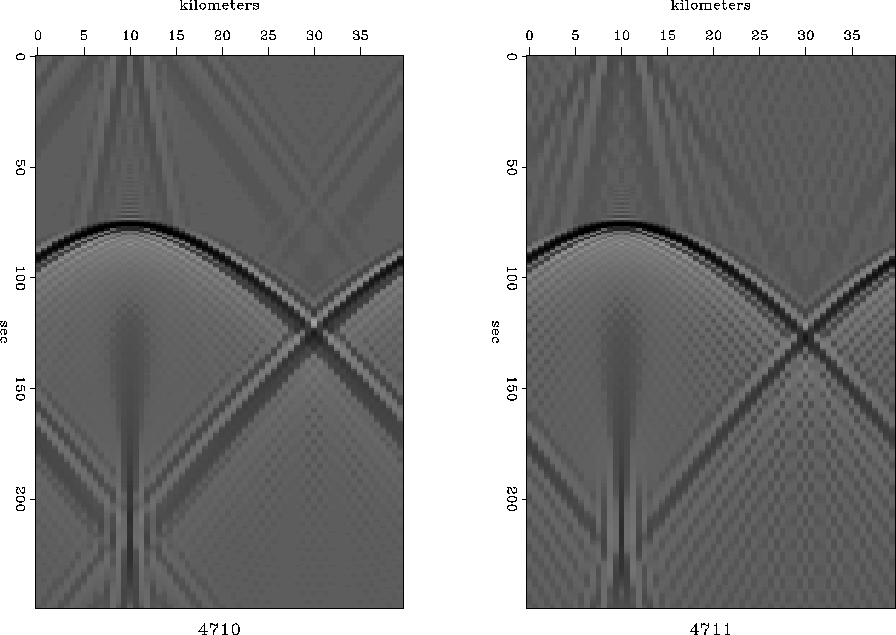What do you think?

Complete as this analysis must seem, it is limited by the assumption of Fourier analysis that velocity is constant laterally. To handle this problem we turn now to the final lecture on techniques.