Next: Gain control does dip
Up: COSMETIC ASPECT OF WAVE
Previous: Accentuating faults
Dip filtering is conveniently incorporated
into the wave extrapolation equations.
Instead of initializing the Muir expansion
with 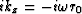 we use
we use
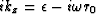 .(Recall from chapter
.(Recall from chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) that r0 is the cosine
of an exactly fitting angle).
For the 15
that r0 is the cosine
of an exactly fitting angle).
For the 15 equation we have
equation we have
| 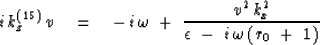 |
(6) |
For the 45 equation we have
equation we have
| 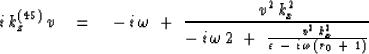 |
(7) |
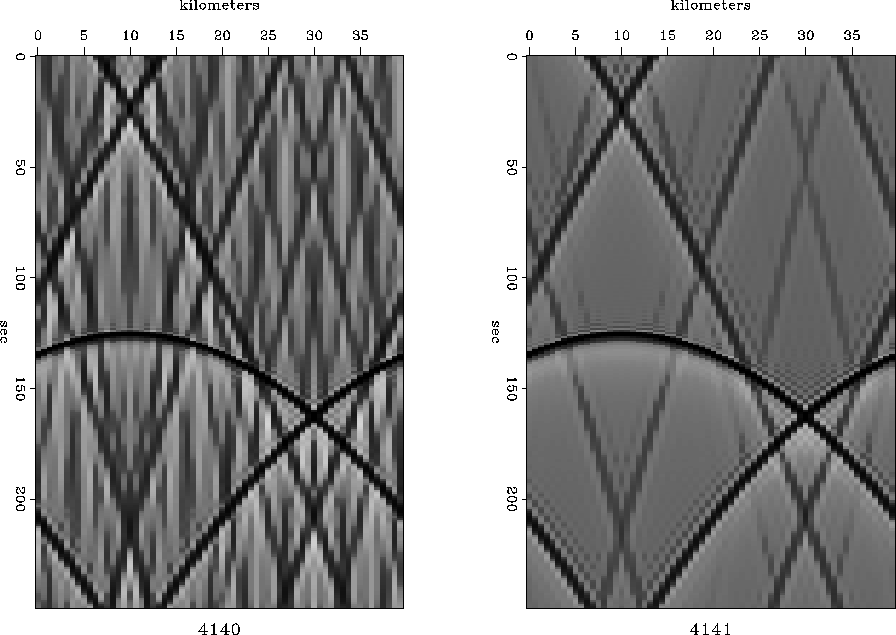
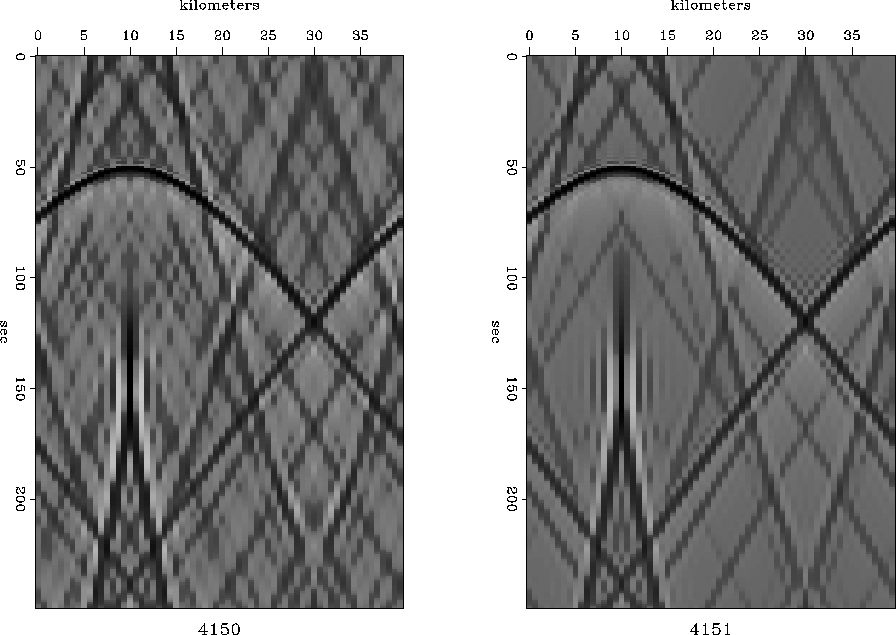
Figures 5 and 6 show
hyperbolas of diffraction for
the 15 and 45
and 45 equations
with and without the dip filtering parameter
equations
with and without the dip filtering parameter  .
.
hyp15
Figure 5
Diffraction hyperbolas of the 15 equation
without dip filtering (left),
and with dip filtering (right).
equation
without dip filtering (left),
and with dip filtering (right).





hyp45
Figure 6
Diffraction hyperbolas of the 45 equation
without dip filtering (left),
and with dip filtering (right).
equation
without dip filtering (left),
and with dip filtering (right).










Next: Gain control does dip
Up: COSMETIC ASPECT OF WAVE
Previous: Accentuating faults
Stanford Exploration Project
10/31/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) that r0 is the cosine
of an exactly fitting angle).
For the 15
that r0 is the cosine
of an exactly fitting angle).
For the 15![]() we use
we use
![]() .(Recall from chapter
.(Recall from chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) that r0 is the cosine
of an exactly fitting angle).
For the 15
that r0 is the cosine
of an exactly fitting angle).
For the 15![]() equation we have
equation we have
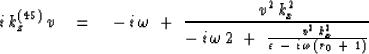
![]() and 45
and 45![]() equations
with and without the dip filtering parameter
equations
with and without the dip filtering parameter ![]() .
.