 |
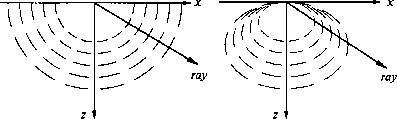
Figure 7 Wavefronts in an isotropic medium (left) and an anisotropic medium (right). Note that on the right, the rays are not perpendicular to the wavefronts. (Rothman)
Anisotropy means that waves propagating in different directions propagate at different speeds. Anisotropy does not mean that velocity is a function of spatial location, and thus anisotropy does not cause rays to bend. The peculiar thing about anisotropy is that rays are not perpendicular to wavefronts. Figure 7 illustrates this idea.
 |
The diagram on the left shows spherical wavefronts emanating from a point
source at the origin.
This is the usual, isotropic case.
The diagram on the right shows the nonspherical wavefronts
of the 15![]() migration equation.
Note that near the z-axis they are nearly spherical,
but further away they do a poor job of matching a sphere with
its center at the origin.
migration equation.
Note that near the z-axis they are nearly spherical,
but further away they do a poor job of matching a sphere with
its center at the origin.
The ideal wavefront from a Huygens secondary source is a semicircle.
The secondary source that results from the 15![]() extrapolation equation is an ellipse.
The secondary source that results from the 45
extrapolation equation is an ellipse.
The secondary source that results from the 45![]() extrapolation equation is an interesting, heartlike shape. These are
drawn in Figure 8.
extrapolation equation is an interesting, heartlike shape. These are
drawn in Figure 8.
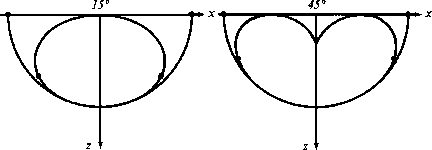 |
In practice, the top parts of the ellipse and the heart are rarely
observed because they are in the evanescent zone,
and the x-axis is seldom refined enough for them to be below
the aliasing frequency.
The center of the heart is sometimes seen in
the (x,t)-plane when the
45![]() program is used.
It is shown by a line drawing in Figure 9
and shown using a 45
program is used.
It is shown by a line drawing in Figure 9
and shown using a 45![]() diffraction program in Figure 16.
diffraction program in Figure 16.
|
anisoxt
Figure 9 45 |  |