




Next: About this document ...
Up: THE BULLETPROOFING OF MUIR
Previous: Stability of the difference
The scalar wave equation for the extrapolation of a downgoing wavefield is
| 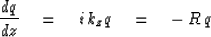 |
(87) |
where the R operator takes the usual form
| 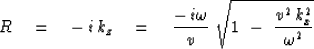 |
(88) |
Our plan is to approximate the square root
by the usual continued fraction expansion
and then identify 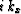 with
with 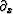 to obtain
a space-domain equation.
The main effort we must make stems from our refusal to
make the usual assumption that v(x,z) is
independent of x.
Since
to obtain
a space-domain equation.
The main effort we must make stems from our refusal to
make the usual assumption that v(x,z) is
independent of x.
Since 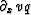 differs from
differs from 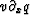 , the space representation does not seem
to be unique, and we may wonder how the
variable q relates to physical
wave variables like pressure and displacement.
Since (88) is purely imaginary,
the depth-invariance of the quadratic
, the space representation does not seem
to be unique, and we may wonder how the
variable q relates to physical
wave variables like pressure and displacement.
Since (88) is purely imaginary,
the depth-invariance of the quadratic 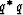 can be interpreted
as the downward energy flux
across the datum at depth z.
Our main effort will be to assure that
can be interpreted
as the downward energy flux
across the datum at depth z.
Our main effort will be to assure that 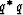 does indeed remain depth-invariant when
does indeed remain depth-invariant when 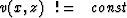 .The task of determining the relation between the
energy flux variable q and
the physical variables will be left to the reader.
.The task of determining the relation between the
energy flux variable q and
the physical variables will be left to the reader.
First v2 kx2 must be represented in the space domain.
Thinking of the x-derivative
operator 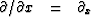 as a large
bidiagonal matrix with
as a large
bidiagonal matrix with 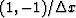 along the diagonal
and V(x) as a diagonal matrix, we are attracted to expressions
like
along the diagonal
and V(x) as a diagonal matrix, we are attracted to expressions
like 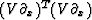 or
or 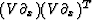 because they are symmetric, positive, semidefinite matrices.
In simplest form, such numerical representations are tridiagonal matrices that
can be abbreviated as either
because they are symmetric, positive, semidefinite matrices.
In simplest form, such numerical representations are tridiagonal matrices that
can be abbreviated as either
| 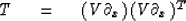 |
(89) |
or
| 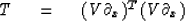 |
(90) |
At a later time accuracy or some other consideration
could determine the choice in (89) and (90).
Even other expressions could be used,
provided they are real, symmetric, and positive definite.
In the previous section
the constant velocity, 45 expansion of (88) was shown to be
expansion of (88) was shown to be
| 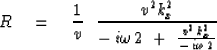 |
(91) |
This scalar R always has a positive real part
because 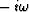 is always represented in an impedance form,
and the whole expression is built up satisfying Muir's rules
for combining impedance functions.
In going to the x-domain notice
that
is always represented in an impedance form,
and the whole expression is built up satisfying Muir's rules
for combining impedance functions.
In going to the x-domain notice
that 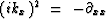 and
and 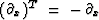 .So the positive scalar v2 kx2 corresponds to the positive
eigenvalues of (89) and (90).
.So the positive scalar v2 kx2 corresponds to the positive
eigenvalues of (89) and (90).
The expression of the bulletproof, square-root
operator R in the space domain will now be given as
| 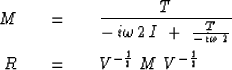 |
(92) |
| (93) |
Use of the division sign in (92) and (93)
is justifiable
because the matrix T commutes with the identity matrix I.
(A hazard in this work is that T does not
commute with the diagonal matrix V).
The matrix M has the properties
required of R since a basic matrix theorem
says that the eigenvalues of a polynomial of a real symmetric matrix are the
polynomials of the eigenvalues.
In other words, replacing T in (92) and (93)
by one of its eigenvalues produces a
complex M whose real part is positive,
so that 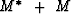 is positive as required.
What is needed is to show that the following matrix is positive definite:
is positive as required.
What is needed is to show that the following matrix is positive definite:
| 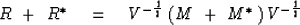 |
(94) |
A matrix A is positive definite if
for arbitrary d, the scalar 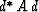 is positive.
The diagonal matrix
is positive.
The diagonal matrix 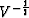 can certainly be
absorbed into d and d will still be
arbitrary, so the proof is complete.
can certainly be
absorbed into d and d will still be
arbitrary, so the proof is complete.
In programming it is a nuisance to put 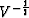 on each side of the matrix M.
Actually you can put V-1 on either side.
In general, some other quadratic form such as
on each side of the matrix M.
Actually you can put V-1 on either side.
In general, some other quadratic form such as
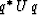 where U is
strictly positive definite
will be decreasing if
where U is
strictly positive definite
will be decreasing if
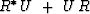 is positive definite.
is positive definite.





Next: About this document ...
Up: THE BULLETPROOFING OF MUIR
Previous: Stability of the difference
Stanford Exploration Project
10/31/1997
![]() with
with ![]() to obtain
a space-domain equation.
The main effort we must make stems from our refusal to
make the usual assumption that v(x,z) is
independent of x.
Since
to obtain
a space-domain equation.
The main effort we must make stems from our refusal to
make the usual assumption that v(x,z) is
independent of x.
Since ![]() differs from
differs from ![]() , the space representation does not seem
to be unique, and we may wonder how the
variable q relates to physical
wave variables like pressure and displacement.
Since (88) is purely imaginary,
the depth-invariance of the quadratic
, the space representation does not seem
to be unique, and we may wonder how the
variable q relates to physical
wave variables like pressure and displacement.
Since (88) is purely imaginary,
the depth-invariance of the quadratic ![]() can be interpreted
as the downward energy flux
across the datum at depth z.
Our main effort will be to assure that
can be interpreted
as the downward energy flux
across the datum at depth z.
Our main effort will be to assure that ![]() does indeed remain depth-invariant when
does indeed remain depth-invariant when ![]() .The task of determining the relation between the
energy flux variable q and
the physical variables will be left to the reader.
.The task of determining the relation between the
energy flux variable q and
the physical variables will be left to the reader.
![]() as a large
bidiagonal matrix with
as a large
bidiagonal matrix with ![]() along the diagonal
and V(x) as a diagonal matrix, we are attracted to expressions
like
along the diagonal
and V(x) as a diagonal matrix, we are attracted to expressions
like ![]() or
or ![]() because they are symmetric, positive, semidefinite matrices.
In simplest form, such numerical representations are tridiagonal matrices that
can be abbreviated as either
because they are symmetric, positive, semidefinite matrices.
In simplest form, such numerical representations are tridiagonal matrices that
can be abbreviated as either
![]() expansion of (88) was shown to be
expansion of (88) was shown to be
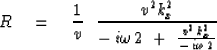
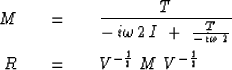
![]() on each side of the matrix M.
Actually you can put V-1 on either side.
In general, some other quadratic form such as
on each side of the matrix M.
Actually you can put V-1 on either side.
In general, some other quadratic form such as
![]() where U is
strictly positive definite
will be decreasing if
where U is
strictly positive definite
will be decreasing if
![]() is positive definite.
is positive definite.