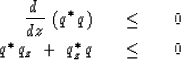Next: Stability of the difference
Up: THE BULLETPROOFING OF MUIR
Previous: THE BULLETPROOFING OF MUIR
Let 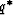 denote the
Hermitian conjugate of q.
For equation (80) to be stable
the energy
denote the
Hermitian conjugate of q.
For equation (80) to be stable
the energy 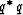 must be either constant or
decaying during depth extrapolation.
must be either constant or
decaying during depth extrapolation.
| 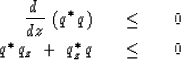 |
|
| (82) |
Substituting equation (80) into equation (82) gives
| 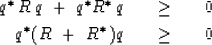 |
|
| (83) |
Equation (83) shows that 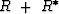 must be positive semidefinite
for the differential equation to be stable.
must be positive semidefinite
for the differential equation to be stable.





Next: Stability of the difference
Up: THE BULLETPROOFING OF MUIR
Previous: THE BULLETPROOFING OF MUIR
Stanford Exploration Project
10/31/1997
![]() denote the
Hermitian conjugate of q.
For equation (80) to be stable
the energy
denote the
Hermitian conjugate of q.
For equation (80) to be stable
the energy ![]() must be either constant or
decaying during depth extrapolation.
must be either constant or
decaying during depth extrapolation.