




Next: Coding multidimensional de/convolution
Up: FILTERING ON A HELIX
Previous: Multidimensional deconvolution breakthrough
Let us associate x- and y-derivatives with
a finite-difference stencil or template.
(For simplicity take 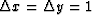 .)
.)
| 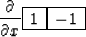 |
(3) |
| 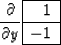 |
(4) |
Convolving a data plane with
the stencil (3)
forms the x-derivative of the plane.
Convolving a data plane with
the stencil (4)
forms the y-derivative of the plane.
On the other hand,
deconvolving
with (3) integrates data along the x-axis for each y.
Likewise, deconvolving
with (4) integrates data along the y-axis for each x.
Next we look at a fully two-dimensional operator
(like the cross derivative 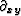 ).
).
A nontrivial two-dimensional convolution stencil is
| 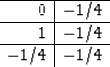 |
(5) |
We will convolve and deconvolve a data plane with this operator.
Although everything is shown on a plane,
the actual computations are done in one dimension
with equations
(1) and
(2).
Let us manufacture the simple data plane
shown on the left in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Beginning with a zero-valued plane, we add
in a copy of the filter (5)
near the top of the frame.
Nearby add another copy with opposite polarity.
Finally add some impulses near the bottom boundary.
The second frame in Figure
.
Beginning with a zero-valued plane, we add
in a copy of the filter (5)
near the top of the frame.
Nearby add another copy with opposite polarity.
Finally add some impulses near the bottom boundary.
The second frame in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the result
of deconvolution by the filter (5)
using the one-dimensional equation (2).
Notice that deconvolution
turns the filter itself into an impulse,
while it turns the impulses
into comet-like images.
The use of a helix is evident
by the comet images wrapping around the vertical axis.
wrap90
is the result
of deconvolution by the filter (5)
using the one-dimensional equation (2).
Notice that deconvolution
turns the filter itself into an impulse,
while it turns the impulses
into comet-like images.
The use of a helix is evident
by the comet images wrapping around the vertical axis.
wrap90
Figure 3
Illustration of 2-D deconvolution.
Left is the input.
Right is after deconvolution with
the filter (5)
as preformed by
by module
polydiv





The filtering in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ran along a helix from left to right.
Figure
ran along a helix from left to right.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a second filtering running from right to left.
Filtering in the reverse direction is the adjoint.
After deconvolving both ways, we have accomplished a symmetical smoothing.
The final frame undoes the smoothing to bring us exactly back
to where we started.
The smoothing was done with two passes of deconvolution
and it is undone by two passes of convolution.
No errors, no evidence remains of any of the boundaries
where we have wrapped and truncated.
shows a second filtering running from right to left.
Filtering in the reverse direction is the adjoint.
After deconvolving both ways, we have accomplished a symmetical smoothing.
The final frame undoes the smoothing to bring us exactly back
to where we started.
The smoothing was done with two passes of deconvolution
and it is undone by two passes of convolution.
No errors, no evidence remains of any of the boundaries
where we have wrapped and truncated.
hback90
Figure 4
Recursive filtering backwards (leftward on the space axis)
is done by the adjoint of 2-D deconvolution.
Here we see that 2-D deconvolution compounded with its adjoint
is exactly inverted by 2-D convolution and its adjoint.





Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) explains the important practical role
to be played by a multidimensional operator for which
we know the exact inverse.
Other than multidimensional Fourier transformation,
transforms based on polynomial multiplication and division
on a helix are the only known easily invertible linear operators.
explains the important practical role
to be played by a multidimensional operator for which
we know the exact inverse.
Other than multidimensional Fourier transformation,
transforms based on polynomial multiplication and division
on a helix are the only known easily invertible linear operators.
In seismology we often have occasion to steer summation along beams.
Such an impulse response is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
waves90
Figure 5
A simple low-order 2-D filter whose inverse
contains plane waves of two different dips.
One of them is spatially aliased.
|
|  |





Of special interest are filters that destroy plane waves.
The inverse of such a filter creates plane waves.
Such filters are like wave equations.
A filter that creates two plane waves is illustrated in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
dip90
Figure 6
A simple low-order 2-D filter whose inverse times its inverse adjoint,
is approximately a dipping seismic arrival.










Next: Coding multidimensional de/convolution
Up: FILTERING ON A HELIX
Previous: Multidimensional deconvolution breakthrough
Stanford Exploration Project
4/27/2004
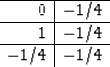
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Beginning with a zero-valued plane, we add
in a copy of the filter (5)
near the top of the frame.
Nearby add another copy with opposite polarity.
Finally add some impulses near the bottom boundary.
The second frame in Figure
.
Beginning with a zero-valued plane, we add
in a copy of the filter (5)
near the top of the frame.
Nearby add another copy with opposite polarity.
Finally add some impulses near the bottom boundary.
The second frame in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the result
of deconvolution by the filter (5)
using the one-dimensional equation (2).
Notice that deconvolution
turns the filter itself into an impulse,
while it turns the impulses
into comet-like images.
The use of a helix is evident
by the comet images wrapping around the vertical axis.
is the result
of deconvolution by the filter (5)
using the one-dimensional equation (2).
Notice that deconvolution
turns the filter itself into an impulse,
while it turns the impulses
into comet-like images.
The use of a helix is evident
by the comet images wrapping around the vertical axis.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ran along a helix from left to right.
Figure
ran along a helix from left to right.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a second filtering running from right to left.
Filtering in the reverse direction is the adjoint.
After deconvolving both ways, we have accomplished a symmetical smoothing.
The final frame undoes the smoothing to bring us exactly back
to where we started.
The smoothing was done with two passes of deconvolution
and it is undone by two passes of convolution.
No errors, no evidence remains of any of the boundaries
where we have wrapped and truncated.
shows a second filtering running from right to left.
Filtering in the reverse direction is the adjoint.
After deconvolving both ways, we have accomplished a symmetical smoothing.
The final frame undoes the smoothing to bring us exactly back
to where we started.
The smoothing was done with two passes of deconvolution
and it is undone by two passes of convolution.
No errors, no evidence remains of any of the boundaries
where we have wrapped and truncated.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) explains the important practical role
to be played by a multidimensional operator for which
we know the exact inverse.
Other than multidimensional Fourier transformation,
transforms based on polynomial multiplication and division
on a helix are the only known easily invertible linear operators.
explains the important practical role
to be played by a multidimensional operator for which
we know the exact inverse.
Other than multidimensional Fourier transformation,
transforms based on polynomial multiplication and division
on a helix are the only known easily invertible linear operators.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
