Review of 1-D recursive filters

Convolution is the operation we do on polynomial coefficients when we multiply polynomials. Deconvolution is likewise for polynomial division. Often these ideas are described as polynomials in the variable Z. Take X(Z) to denote the polynomial whose coefficients are samples of input data, and let A(Z) likewise denote the filter. The convention I adopt here is that the first coefficient of the filter has the value +1, so the filter's polynomial is 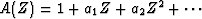$A(Z) = 1 + a_1Z + a_2Z^2 + \cdots$.To see how to convolve, we now identify the coefficient of Z^k in the product Y(Z)=A(Z)X(Z). The usual case (k larger than the number N_a of filter coefficients) is  

$$y_k \quad=\quad x_k + \sum_{i=1}^{N_a} a_i x_{k-i}$$ (1)

Convolution computes y_k from x_k whereas deconvolution (also called back substitution) does the reverse. Rearranging (1) we get  

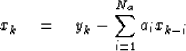$$x_k \quad=\quad y_k - \sum_{i=1}^{N_a} a_i x_{k-i}$$ (2)

where now we are finding the output x_k from its past outputs x_k-i and from the present input y_k. We see that the deconvolution process is essentially the same as the convolution process, except that the filter coefficients are used with opposite polarity; and they are applied to the past outputs instead of the past inputs. That is why deconvolution must be done sequentially while convolution can be done in parallel.