Next: About this document ...
Up: One-sided functions
Previous: NOTCH FILTER AND POLE
Z transforms and Fourier transforms are related
by the relations 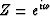 and
and
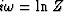 .A problem with these relations is that
simple ratios of polynomials in Z do not translate to
ratios of polynomials in
.A problem with these relations is that
simple ratios of polynomials in Z do not translate to
ratios of polynomials in 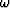 and vice versa. The
approximation
and vice versa. The
approximation
| 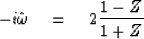 |
(42) |
is easily solved for Z as
| 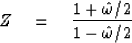 |
(43) |
These approximations are often useful.
They are truncations of the exact power series expansions
| ![\begin{displaymath}
-i\omega
\eq - \, \ln \, e^{i\omega}
\eq -\ln \, Z
\eq 2 \le...
...er 3}
{(1 - Z)^3 \over (1 + Z)^3}
+ {1 \over 5} \cdots \right]\end{displaymath}](img122.gif) |
(44) |
and
| 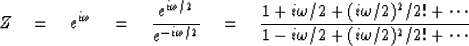 |
(45) |
For a Z transform B(Z) to be minimum phase,
any root Z0 of 0 = B(Z0) should be outside the
unit circle. Since
![$Z_0 = \exp \{i[\mbox{Re} (\omega_0) + i\, \mbox{Im} (\omega_0)]\} $](img124.gif) and
and 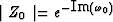 , it means
that for a minimum phase
, it means
that for a minimum phase 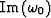 should be
negative. (In other words,
should be
negative. (In other words, 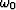 is in the lower
half-plane.) Thus it may be said that
is in the lower
half-plane.) Thus it may be said that
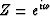 maps the exterior of the unit circle
to the lower half-plane. By inspection of
Figures 20 and 21, it is found
that the bilinear approximation (42) or
(43) also maps the exterior of the unit
circle into the lower half-plane.
maps the exterior of the unit circle
to the lower half-plane. By inspection of
Figures 20 and 21, it is found
that the bilinear approximation (42) or
(43) also maps the exterior of the unit
circle into the lower half-plane.
 2-21
2-21
Figure 21
The points of Figure 20
displayed in the Z plane,
the 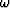 plane, and the
plane, and the 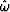 -plane.
-plane.

Thus, although the bilinear approximation is an
approximation, it turns out to exactly preserve
the minimum-phase property. This is very
fortunate because if a stable differential equation
is converted to a difference equation via
(42), the resulting difference equation will be stable.
(Many cases may be found where the
approximation of a time derivative by multiplication
with 1 - Z would convert a stable differential
equation into an unstable difference equation.)
A handy way to remember (42) is that
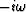 corresponds to time differentiation
of a Fourier transform and (1 - Z) is the
first differencing operator. The (1 + Z) in
the denominator gets things ``centered" at
Z1/2
corresponds to time differentiation
of a Fourier transform and (1 - Z) is the
first differencing operator. The (1 + Z) in
the denominator gets things ``centered" at
Z1/2
To see that the bilinear approximation is a
low-frequency approximation, multiply
top and bottom of (42) by Z-1/2
| 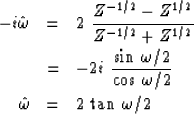 |
|
| |
| (46) |
Equation (46) implicitly refers to
a sampling rate of one sample per second. Taking an
arbitrary sampling rate 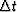 , the approximation
(46) becomes
, the approximation
(46) becomes
| 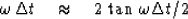 |
(47) |
This approximation is plotted in Figure 22.
Clearly, the error can be made as small as one wishes merely
by sampling often enough; that is, taking 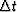 small enough.
small enough.
2-22
Figure 22
The accuracy of the bilinear transformation approximation.
|
|  |

From Figure 22 we see that the
error will be only a few percent if we choose
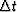 small enough so that
small enough so that
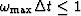 . Readers
familiar with the folding theorem will recall
that it gives the less severe restraint
. Readers
familiar with the folding theorem will recall
that it gives the less severe restraint
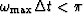 . Clearly,
the folding theorem is too generous for
applications involving the bilinear transform.
. Clearly,
the folding theorem is too generous for
applications involving the bilinear transform.
Now, by way of example, let us take up the case
of a pole 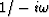 at zero frequency.
This is integration. For reasons which will presently
be clear, we will consider the slightly different pole
at zero frequency.
This is integration. For reasons which will presently
be clear, we will consider the slightly different pole
| 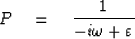 |
(48) |
where  is small. Inserting
the bilinear transform, we get
is small. Inserting
the bilinear transform, we get
| ![\begin{eqnarray}
P
&= & {1 \over 2 [(1 - Z)/(1 + Z)] + \varepsilon}
\eq {0.5(1...
...& {0.5(1 + Z) \over (1 + \varepsilon /2)
- Z(1 - \varepsilon /2)}\end{eqnarray}](img136.gif) |
|
| (49) |
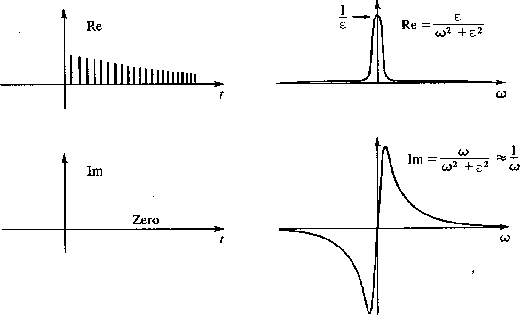
By inspection of (49) we see that the
time-domain function is real, and as  goes
to zero it takes the form (.5, 1, 1, 1, ...). (Taking
goes
to zero it takes the form (.5, 1, 1, 1, ...). (Taking
 positive forces the step to go out into
positive time, whereas
positive forces the step to go out into
positive time, whereas  negative would
cause the step to rise at negative time.) The
properties of this function are summarized in
Figure 23.
2-23
negative would
cause the step to rise at negative time.) The
properties of this function are summarized in
Figure 23.
2-23
Figure 23
Properties of the integration operator.

EXERCISES:
- In the solution to diffusion problems,
the factor
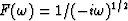 often
arises as a multiplier. To see the equivalent
convolution operation, find a causal, sampled-time
representation ft of
often
arises as a multiplier. To see the equivalent
convolution operation, find a causal, sampled-time
representation ft of 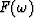 by identification
of powers of Z in
Solve numerically for f0 through f7.
by identification
of powers of Z in
Solve numerically for f0 through f7.





Next: About this document ...
Up: One-sided functions
Previous: NOTCH FILTER AND POLE
Stanford Exploration Project
10/30/1997
![]() and
and
![]() .A problem with these relations is that
simple ratios of polynomials in Z do not translate to
ratios of polynomials in
.A problem with these relations is that
simple ratios of polynomials in Z do not translate to
ratios of polynomials in ![]() and vice versa. The
approximation
and vice versa. The
approximation
![]() and
and ![]() , it means
that for a minimum phase
, it means
that for a minimum phase ![]() should be
negative. (In other words,
should be
negative. (In other words, ![]() is in the lower
half-plane.) Thus it may be said that
is in the lower
half-plane.) Thus it may be said that
![]() maps the exterior of the unit circle
to the lower half-plane. By inspection of
Figures 20 and 21, it is found
that the bilinear approximation (42) or
(43) also maps the exterior of the unit
circle into the lower half-plane.
maps the exterior of the unit circle
to the lower half-plane. By inspection of
Figures 20 and 21, it is found
that the bilinear approximation (42) or
(43) also maps the exterior of the unit
circle into the lower half-plane.
![]() corresponds to time differentiation
of a Fourier transform and (1 - Z) is the
first differencing operator. The (1 + Z) in
the denominator gets things ``centered" at
Z1/2
corresponds to time differentiation
of a Fourier transform and (1 - Z) is the
first differencing operator. The (1 + Z) in
the denominator gets things ``centered" at
Z1/2
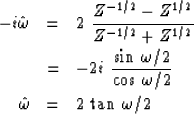
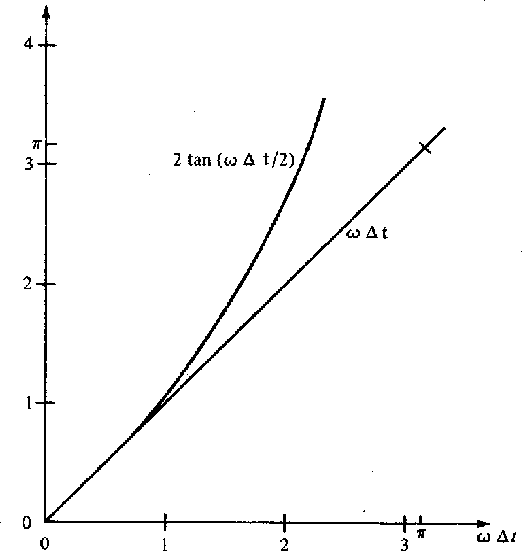
![]() small enough so that
small enough so that
![]() . Readers
familiar with the folding theorem will recall
that it gives the less severe restraint
. Readers
familiar with the folding theorem will recall
that it gives the less severe restraint
![]() . Clearly,
the folding theorem is too generous for
applications involving the bilinear transform.
. Clearly,
the folding theorem is too generous for
applications involving the bilinear transform.
![]() at zero frequency.
This is integration. For reasons which will presently
be clear, we will consider the slightly different pole
at zero frequency.
This is integration. For reasons which will presently
be clear, we will consider the slightly different pole
![\begin{eqnarray}
P
&= & {1 \over 2 [(1 - Z)/(1 + Z)] + \varepsilon}
\eq {0.5(1...
...& {0.5(1 + Z) \over (1 + \varepsilon /2)
- Z(1 - \varepsilon /2)}\end{eqnarray}](img136.gif)