NOTCH FILTER AND POLE ON PEDESTAL

In some applications it is desired to reject a very narrow frequency band leaving the rest of the spectrum little changed. The most common example is 60-Hz noise from power lines. Such a filter can easily be made with a slight variation on the all-pass filter. In the all-pass filter the pole and zero have an equal (logarithmic) relative distance from the unit circle. All we need to do is to put the zero closer to the circle. In fact, there is no reason why we should not put the zero right on the circle. Then the frequency at which the zero is located is exactly canceled from the spectrum of input data. If the undesired frequency need not be completely rejected, then the zero can be left just inside or outside the circle. As the zero is moved farther away from the circle, the notch becomes less deep until finally the zero is farther from the circle than the pole and the notch has become a hump. The resulting filter which will be called pole on pedestal is in many respects like the narrowband filter discussed earlier. Some of these filters are illustrated in Figures 18 and 19. The difference between the pole-on-pedestal and the narrowband filters is in the asymptotic behavior away from $\omega_0$. The former is flat, while the latter continues to decay with increasing $\mid \omega - \omega_0 \mid$. This makes the pole on pedestal more convenient for creating complicated filter shapes by cascades of single-pole filters.

 

2-18 Figure 18 Pole and zero locations for some simple filters. Circles are unit circles in the Z plane. Poles are marked by X and zeros by 0.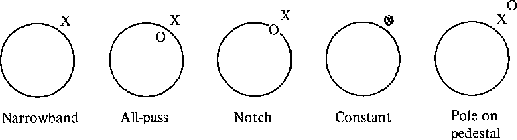

 

2-19 Figure 19 Amplitude vs. frequency for narrowband filter (NB) and pole-on-pedestal filter (PP). Each has one pole at 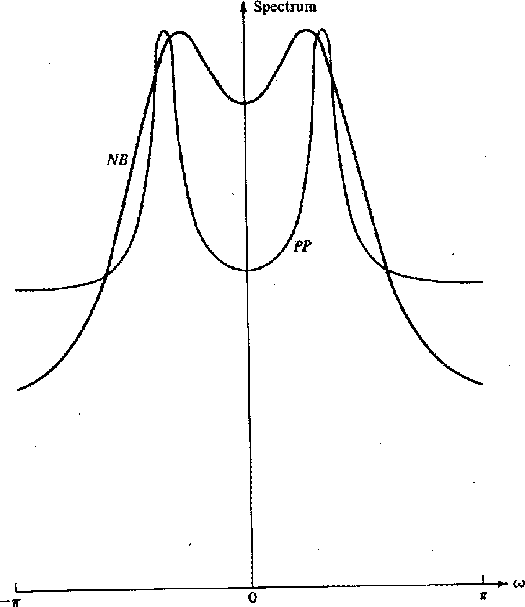$Z_0 = 1.2e^{i\pi /3}$. A second pole at $Z_0 = 1.2e^{-i\pi /3}$ enables the filters to be real in the time domain.

Narrowband filters and sharp cutoff filters should be used with caution. An ever-present penalty for such filters is that they do not decay rapidly in time. Although this may not present problems in some applications, it will do so in others. Obviously, if the data collection duration is shorter or comparable to the impulse response of the narrowband filter, then the transient effects of starting up the experiment will not have time to die out. Likewise, the notch should not be too narrow in a 60-Hz rejection filter. Even a bandpass filter (easier to implement with fast Fourier transform than with a few poles) has a certain decay rate in the time domain which may be too slow for some experiments. In radar and in reflection seismology the importance of a signal is not related to its strength. Late-arriving echoes may be very weak, but they contain information not found in earlier echoes. If too sharp a frequency characteristic is used, then filter resonance from early strong arrivals may not have decayed sufficiently by the time that the weak late echoes arrive.

EXERCISES:

1. Consider a symmetric (nonrealizable) filter which passes all frequencies less than $\omega_0$ with unit gain. Frequencies above $\omega_0$ are completely attenuated. What is the rate of decay of amplitude with time for this filter?
2. Waves spreading from a point source decay in energy as the area on a sphere. The amplitude decays as the square root of energy. This implies a certain decay in time. The time-decay rate is the same if the waves reflect from planar interfaces. To what power of time t do the signal amplitudes decay? For waves backscattered to the source from point reflectors, energy decays as distance to the minus fourth power. What is the associated decay with time?
3. Discuss the use of the filter of Exercise 1 on the data of Exercise 2.
4. Design a single-pole, single-zero notch filter to reject 59 to 61 Hz on data which are sampled at 500 points per second.