Dipping-reflector shifts

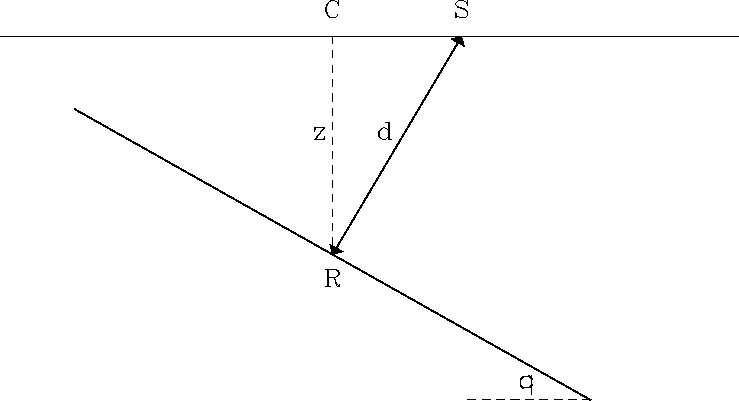
A little geometry gives simple expressions for the horizontal and vertical position errors on the zero-offset section, which are to be corrected by migration. Figure 2 defines the required quantities for a reflection event recorded at S corresponding to the reflectivity at R.

 

reflkine Figure 2 Geometry of the normal ray of length d and the vertical ``shaft'' of length z for a zero-offset experiment above a dipping reflector.

The two-way travel time for the event is related to the length d of the normal ray by  

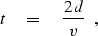$$t \eq {2\,d \over v} \ \ ,$$ (1)

where v is the constant propagation velocity. Geometry of the triangle CRS shows that the true depth of the reflector at R is given by  

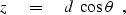$$z \eq d\ \cos\theta \ \ ,$$ (2)

and the lateral shift between true position C and false position S is given by  

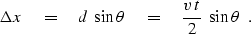$$\Delta x \eq d\ \sin\theta \eq {v\,t \over 2}\ \sin\theta \ \ .$$ (3)

It is conventional to rewrite equation (2) in terms of two-way vertical traveltime $\tau$: 

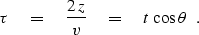$$\tau \eq {2\,z \over v} \eq t\, \cos\theta \ \ .$$ (4)

Thus both the vertical shift 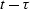$t - \tau$ and the horizontal shift 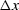$\Delta x$are seen to vanish when the dip angle 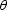$\theta$ is zero.