A dipping reflector

Consider the zero-offset seismic survey shown in Figure 1. This survey uses one source-receiver pair, and the receiver is always at the same location as the source. At each position, denoted by $S_1, S_2, \mbox{and} S_3$ in the figure, the source emits waves and the receiver records the echoes as a single seismic trace. After each trace is recorded, the source-receiver pair is moved a small distance and the experiment is repeated.

 

reflexpt Figure 1 Raypaths and wavefronts for a zero-offset seismic line shot above a dipping reflector. The earth's propagation velocity is constant.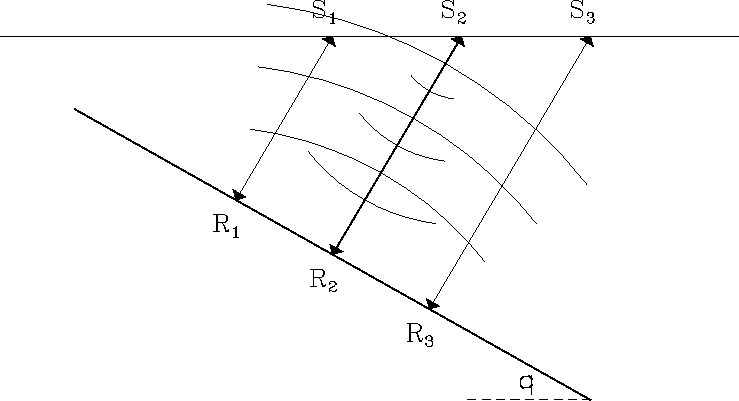

As shown in the figure, the source at S₂ emits a spherically-spreading wave that bounces off the reflector and then returns to the receiver at S₂. The raypaths drawn between S_i and R_i are orthogonal to the reflector and hence are called normal rays.

These rays reveal how the zero-offset section misrepresents the truth. For example, the trace recorded at S₂ is dominated by the reflectivity near reflection point R₂, where the normal ray from S₂ hits the reflector. If the zero-offset section corresponding to Figure 1 is displayed, the reflectivity at R₂ will be falsely displayed as though it were directly beneath S₂, which it certainly is not. This lateral mispositioning is the first part of the illusion. The second part is vertical: if converted to depth, the zero-offset section will show R₂ to be deeper than it really is. The reason is that the slant path of the normal ray is longer than a vertical shaft drilled from the surface down to R₂.