Next: PHASE-SHIFT MIGRATION
Up: DOWNWARD CONTINUATION
Previous: Downward continuation with Fourier
To link Snell waves to Fourier transforms we merge
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
with equations (10)
)
with equations (10)
| 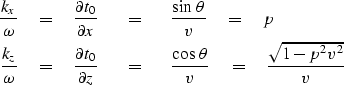 |
(12) |
| (13) |
The basic downward continuation equation for upcoming waves in Fourier space
follows from equation (7) by eliminating p by using
equation (12).
For analysis of real seismic data
we introduce a minus sign because
equation (13) refers to downgoing waves
and observed data is made from up-coming waves.
| 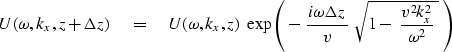 |
(14) |
In Fourier space we delay signals by multiplying by
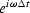 ,analogously, equation (14) says
we downward continue signals into the earth
by multiplying by
,analogously, equation (14) says
we downward continue signals into the earth
by multiplying by 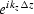 .Multiplication in the Fourier domain
means convolution in time which can be depicted by the engineering diagram
in Figure 5.
inout
.Multiplication in the Fourier domain
means convolution in time which can be depicted by the engineering diagram
in Figure 5.
inout
Figure 5
Downward continuation of a downgoing wavefield.

Downward continuation is a product relationship
in both the  -domain and the kx-domain.
Thus it is a convolution in both time and x.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of x2+z2 - v2 t2.
More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.
-domain and the kx-domain.
Thus it is a convolution in both time and x.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of x2+z2 - v2 t2.
More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.
A nuisance of using Fourier transforms in migration and modeling
is that spaces become periodic.
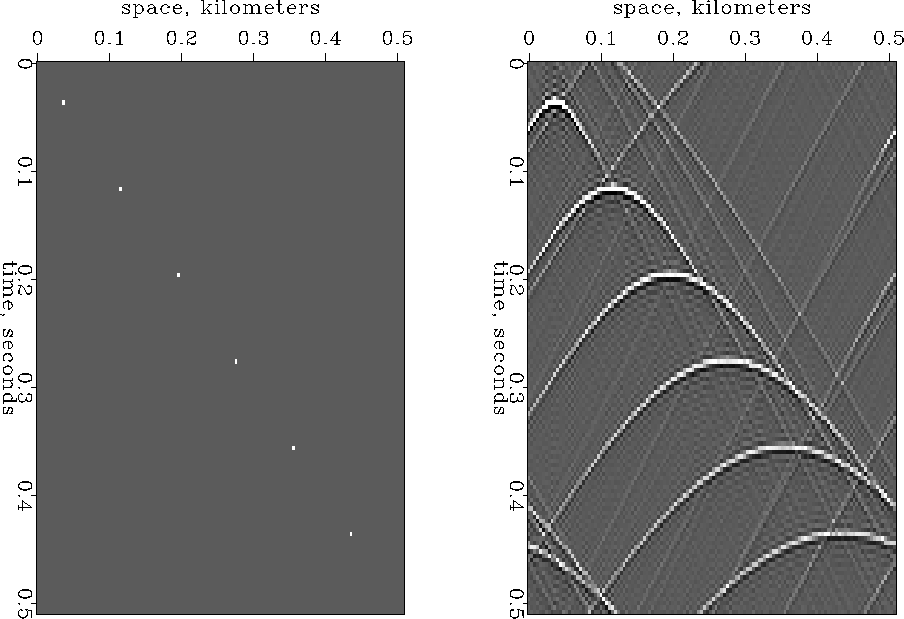
This is demonstrated in Figure 6.
Anywhere an event exits the frame at a side, top, or bottom boundary,
the event immediately emerges on the opposite side.
In practice, the unwelcome effect of periodicity
is generally ameliorated by padding zeros around the data and the model.
diag
Figure 6
A reflectivity model on the left
and synthetic data using a Fourier method on the right.










Next: PHASE-SHIFT MIGRATION
Up: DOWNWARD CONTINUATION
Previous: Downward continuation with Fourier
Stanford Exploration Project
12/26/2000
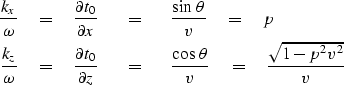
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
with equations (10)
)
with equations (10)
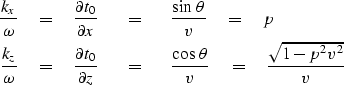
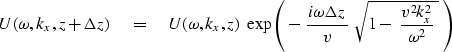
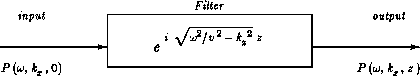
![]() -domain and the kx-domain.
Thus it is a convolution in both time and x.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of x2+z2 - v2 t2.
More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.
-domain and the kx-domain.
Thus it is a convolution in both time and x.
What does the filter look like in the time and space domain?
It turns out like a cone, that is,
it is roughly an impulse function
of x2+z2 - v2 t2.
More precisely, it is the Huygens secondary wave source
that was exemplified by ocean waves entering a gap through a storm barrier.
Adding up the response of multiple gaps in
the barrier would be convolution over x.