




Next: Continuation of a dipping
Up: Downward continuation
Previous: Migration derived from downward
Given a vertically upcoming plane wave
at the earth's surface,
say 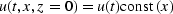 ,and an assumption that the earth's velocity is
vertically stratified, i.e. v=v(z),
we can presume that the upcoming wave down in the earth
is simply time-shifted from what we see on the surface.
(This assumes no multiple reflections.)
Time shifting can be represented as a linear operator in the time domain
by representing it as convolution with an impulse function.
In the frequency domain, time shifting is simply multiplying
by a complex exponential.
This is expressed as
,and an assumption that the earth's velocity is
vertically stratified, i.e. v=v(z),
we can presume that the upcoming wave down in the earth
is simply time-shifted from what we see on the surface.
(This assumes no multiple reflections.)
Time shifting can be represented as a linear operator in the time domain
by representing it as convolution with an impulse function.
In the frequency domain, time shifting is simply multiplying
by a complex exponential.
This is expressed as
| 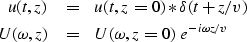 |
(3) |
| (4) |
Sign conventions must be attended to,
and that is explained more fully in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





Next: Continuation of a dipping
Up: Downward continuation
Previous: Migration derived from downward
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.