In a general inhomogeneous medium, finite difference is the most practical method for solving the wave equation. Despite its enormous computational cost, finite-difference schemes provide a comprehensive solution of the wave equation, which includes an accurate representation of amplitude.
In this example, we use the second-order acoustic wave equation for VTI media in ![]() -domain, given by
equation (27) and therefore need to solve simultaneously
-domain, given by
equation (27) and therefore need to solve simultaneously
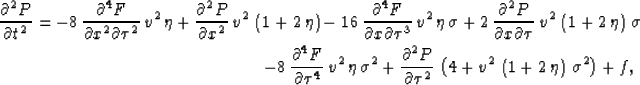 |
||
| (28) |
![]()
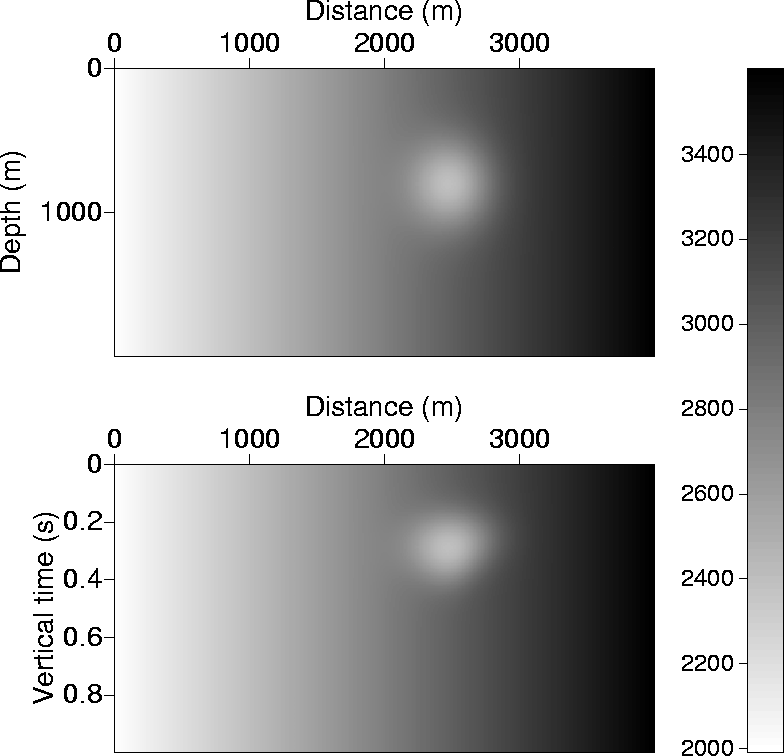 |
Figure 7 shows a velocity model in depth (on the top),
and its equivalent mapping in time (bottom).
Figure 8 shows the wavefield at 0.65 s resulting
a source igniting at time 0 s, that corresponds
to the isotropic velocity model in Figure 7. The wavefield is
computed using finite-difference approximations of equation (26).
The velocity model given in
the ![]() -domain is the input velocity model in the finite-difference
application. This same velocity model
is used to map the wavefield solution back to depth. The solid
curves in Figure 8 show the solution
of the conventional eikonal solver Vidale (1990)
implemented in the depth domain, and these curves nicely envelope the
wavefield solution. Therefore, computing the wavefield in the
-domain is the input velocity model in the finite-difference
application. This same velocity model
is used to map the wavefield solution back to depth. The solid
curves in Figure 8 show the solution
of the conventional eikonal solver Vidale (1990)
implemented in the depth domain, and these curves nicely envelope the
wavefield solution. Therefore, computing the wavefield in the
![]() -domain and in the conventional depth domain
are equivalent, regardless of the lateral inhomogeneity. However, the
-domain and in the conventional depth domain
are equivalent, regardless of the lateral inhomogeneity. However, the ![]() -domain implementation becomes
independent of vertical P-wave velocity when
-domain implementation becomes
independent of vertical P-wave velocity when ![]() .
.
 |
Is is also important to note that the apparent frequency of the time section is velocity independent, while waves in the depth section have wavelengths very much dependent on velocity.