Next: Conclusions
Up: Fomel: Stolt stretch
Previous: ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC
A simple analytic example of isotropic heterogeneity is the case of a
constant velocity gradient. In this
case the velocity distribution can be described by the linear function
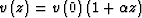 . Stolt stretch transform is found
from (5) as
. Stolt stretch transform is found
from (5) as
| 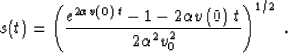 |
(34) |
Let  be the logarithm of the velocity change v(z)/v(0). Then an
explicit expression for W factor follows from (24):
be the logarithm of the velocity change v(z)/v(0). Then an
explicit expression for W factor follows from (24):
| 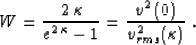 |
(35) |
For
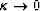 (a small depth or a small velocity gradient),
(a small depth or a small velocity gradient), 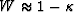 . For
. For
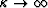 (a large positive change of velocity) W
monotonically approaches zero. Formula (35) can be a useful rule
of thumb for a rough
estimation of W.
(a large positive change of velocity) W
monotonically approaches zero. Formula (35) can be a useful rule
of thumb for a rough
estimation of W.
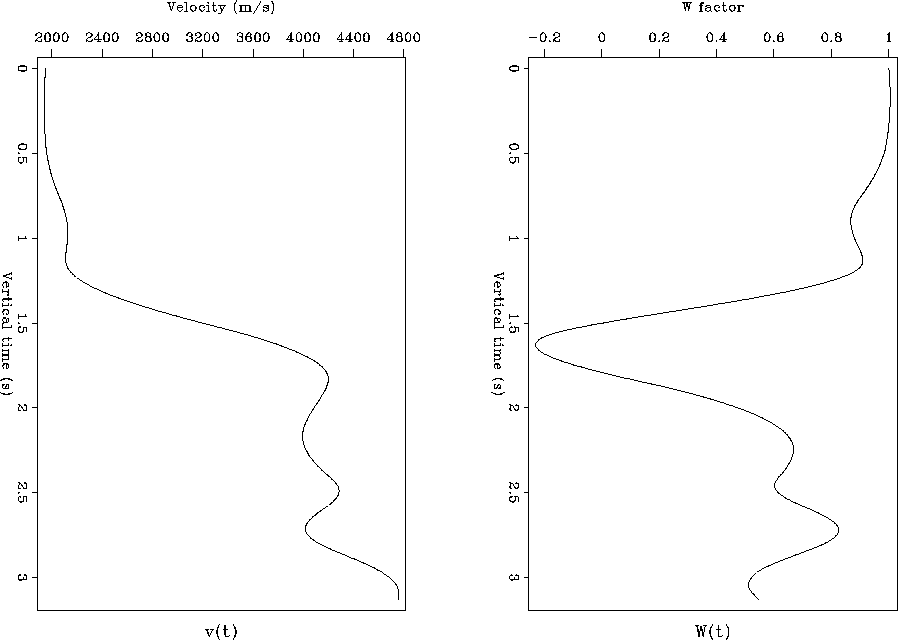
Numerical example of the Stolt stretch parameter computation is
illustrated in Figures 2 and 3. The left side of
Figure 2 shows a smoothed
interval velocity curve from the Gulf of Mexico. The corresponding
optimal values of the W factor as a function of vertical time (in the
isotropic model) are shown on the
right. Though the velocity function is smooth, substantial changes in W
occur, making its mean value for the times 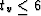 sec equal to
0.631.
sec equal to
0.631.
The theory of cascaded migrations
Beasley et al. (1988); Larner and Beasley (1987) proves that Stolt-type f-k
migration for a nonuniform velocity 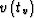 can be
performed as a cascaded process consisting of
migrations with the smaller velocities
can be
performed as a cascaded process consisting of
migrations with the smaller velocities
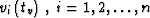 , such that
, such that
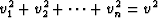 . As shown by Larner and Beasley
1987, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial
. As shown by Larner and Beasley
1987, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial 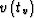 function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
3, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. 1988,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept Fomel (1994). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
3, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. 1988,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept Fomel (1994). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
stovwt
Figure 2 Smoothed interval
velocity distribution from the Gulf of Mexico (left) and the corresponding
W factor as a function of vertical time (right). The mean value of W
is 0.631.




 stocvw
stocvw
Figure 3 Left: Optimal
partitioning of the velocity function for the
method of cascaded migrations. Right: corresponding mean values of
W. Top: four cascaded migrations. Bottom: seven cascaded migrations.










Next: Conclusions
Up: Fomel: Stolt stretch
Previous: ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC
Stanford Exploration Project
4/19/2000
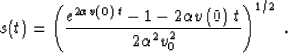
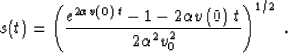
![]() sec equal to
0.631.
sec equal to
0.631.
![]() can be
performed as a cascaded process consisting of
migrations with the smaller velocities
can be
performed as a cascaded process consisting of
migrations with the smaller velocities
![]() , such that
, such that
![]() . As shown by Larner and Beasley
1987, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial
. As shown by Larner and Beasley
1987, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial ![]() function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
3, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. 1988,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept Fomel (1994). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
3, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. 1988,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept Fomel (1994). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.