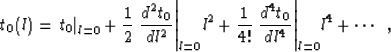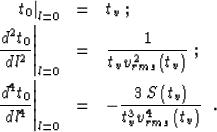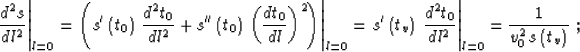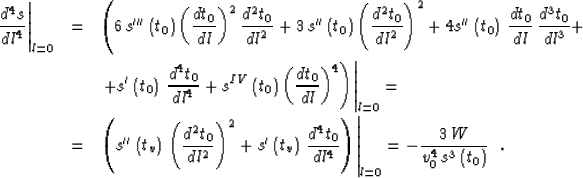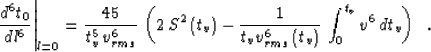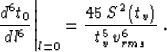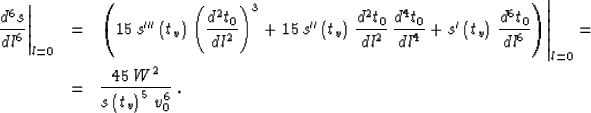Next: ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC
Up: Fomel: Stolt stretch
Previous: STOLT STRETCH THEORY
Formula (11) belongs to the three-parameter class of traveltime
approximations. The key result of this paper uses
a remarkable formal similarity between (11) and
Malovichko's
approximation for the reflection traveltime curve in vertically inhomogeneous
media
Castle (1988); Malovichko (1978); de Bazelaire (1988) defined by
| 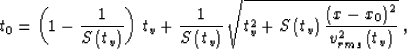 |
(13) |
where vrms stands for the effective (root mean square) velocity along the
vertical
ray
| 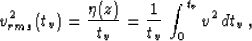 |
(14) |
and S is the parameter of heterogeneity:
| 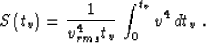 |
(15) |
In terms of the S parameter, the variance of the squared velocity
distribution along the vertical ray
is
| 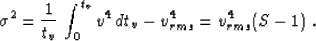 |
(16) |
As follows from equality (16), 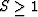 for any type of
velocity distribution
(S
equals 1 in a constant velocity case). For most of the distributions occurring
in
practice, S ranges between 1 and 2.
for any type of
velocity distribution
(S
equals 1 in a constant velocity case). For most of the distributions occurring
in
practice, S ranges between 1 and 2.
Malovichko's formula (13) is known as the
most accurate three-parameter approximation of the NMO curve in vertically
inhomogeneous media.
Since reflection from a horizontal reflector in that class of media is
kinematically
equivalent to diffraction from a point, formula (13)
can be similarly regarded as an approximation of the summation path of the
post-stack Kirchhoff-type migration operator. In this case, it has the same
meaning as formula (11). An important difference between the
two formulae is the fact
that
equation (13) is written in the initial coordinate system and includes coefficients
varying with depth, while equation (11) applies the transformed coordinate system
and
constant coefficients. Using this fact, the rest of this section
compares the accuracy of the approximations and relates Stolt's W factor to
Malovichko's parameter of heterogeneity.
Equations (11) and (13) both approximate the
traveltime
curve in the neighborhood of the vertical ray. Therefore,
to compare their accuracy, it is
appropriate to consider series expansion of the diffraction traveltime in the
vicinity of the vertical ray![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
| 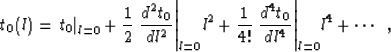 |
(17) |
where l=x-x0.
Expansion (17) contains only even powers of l because of
the obvious symmetry of t0 as a function of l.
The special choice of parameters tv, vrms, and S allows
Malovichko's formula
(13) to provide correct values for the first
three terms of expansion (17):
| 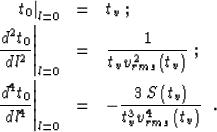 |
(18) |
| (19) |
| (20) |
Considering Levin's formula (11) as an implicit definition of the function
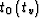 , we can iteratively differentiate it following the
rules of calculus:
, we can iteratively differentiate it following the
rules of calculus:
| 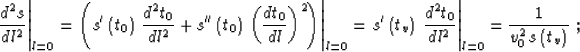 |
(21) |
| 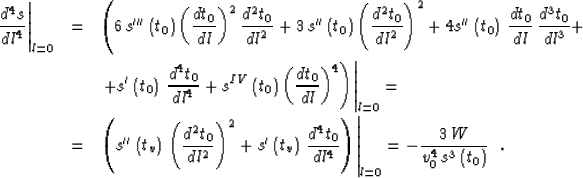 |
|
| |
| (22) |
Substituting the definition of Stolt stretch transform (5) into (21)
produces an equality similar to (19), which means that approximation
(11) is theoretically accurate in depth-varying velocity media up to the
second term in (17). It is this remarkable property that
proves the validity of the Stolt stretch method
Claerbout (1985); Levin (1983). Formula (11) will be
accurate
up to the third term if the value of the fourth-order traveltime derivative in
(22) coincides with (20). Substituting equation (20) into
(22)
transforms the latter to the form
| 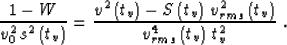 |
(23) |
It is now easy to derive from equation (23) the desired
explicit expression for the
Stolt stretch
parameter W, as follows:
| 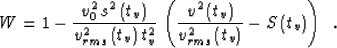 |
(24) |
Expression (24) is derived so as to provide
the best possible value of W for a given depth (vertical time tv). To get a
constant value for a range of depths one should take an average of the right hand
side of
(24) in that range.
The error associated with Stolt stretch can be approximately estimated
from
(17) as the difference between the fourth-order terms:
| 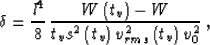 |
(25) |
where 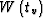 is the right-hand side of (24), and W is the
constant value of W chosen for Stolt migration.
is the right-hand side of (24), and W is the
constant value of W chosen for Stolt migration.
To estimate the best possible
accuracy that the Stolt stretch method can achieve, we must take into
account
the sixth-order
term in (17) related to the sixth-order derivative of the
traveltime curve. For the true traveltime curve,
the expression for the sixth-order derivative in the vicinity of the
vertical ray
is
known from the literature Bolshyh (1956); Taner and Koehler (1969) to be
| 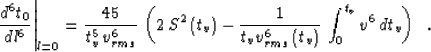 |
(26) |
First, let us estimate the error of Malovichko's approximation (13).
Differentiating (13) six times and setting the offset l to zero yields
| 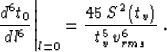 |
(27) |
The estimated error is proportional to the difference between (27) and
(26):
| ![\begin{displaymath}
\delta_M={{l^6} \over {6!}}\,\left[
{{45} \over {t_v^5\, v_{...
...,
\int_0^{t_v} v^6 \,dt_v-S^2\left(t_v\right)
\right)\right]\;.\end{displaymath}](img54.gif) |
(28) |
It is interesting to note that replacing the parameter of heterogeneity S by its definition
(15) changes the expression in the round brackets to the following
form:
| 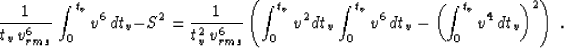 |
(29) |
According to the Schwarz inequality from calculus (
also known as the Cauchy-Bunyakovski inequality), the value
of expression (29) can never
be less
than zero; hence 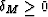 for any velocity distribution. This
conclusion indicates
that Malovichko's approximation tends to increase the traveltime at large
offsets beyond its true value.
for any velocity distribution. This
conclusion indicates
that Malovichko's approximation tends to increase the traveltime at large
offsets beyond its true value.
Differentiating (22) twice and eliminating terms that vanish at l=0 produces
| 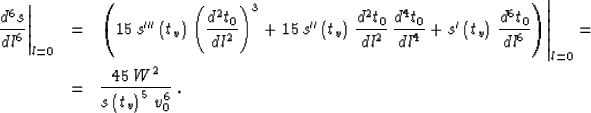 |
|
| (30) |
Evaluating the sixth-order traveltime derivative from (30) and
subtracting
(26), we get a somewhat lengthy but explicit expression for the error
associated
with Stolt stretch approximation in the case of the best possible
choice of W:
| ![\begin{displaymath}
+ {l^6 \over 6!}\,\left[
{{45\, \left( 1-W \right) } \over
...
..._v\right)} \over
{t_v^4\,v_{rms}^8\left(t_v\right)}}
\right]\;.\end{displaymath}](img59.gif) |
(31) |





Next: ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC
Up: Fomel: Stolt stretch
Previous: STOLT STRETCH THEORY
Stanford Exploration Project
4/19/2000
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
: