ABSTRACT
Wavefield extrapolation in the 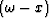 domain provides a tool for
depth migration with strong lateral variations in velocity.
Implicit formulations of depth extrapolation have several advantages
over explicit methods.
However, the simple 3-D extension of conventional 2-D wavefield
extrapolation by implicit finite-differencing requires the
inversion of a 2-D convolution matrix which is computationally
difficult.
In this paper, we solve the 45 wave equation
with helical boundary conditions on one of the spatial axes.
These boundary conditions reduce the 2-D convolution
into an equivalent 1-D filter operation. We then factor this 1-D
filter into causal and anti-causal parts using an extension of
Kolmogoroff's spectral factorization method, and invert the
convolution operator efficiently by 1-D recursive filtering.
We include lateral variations
in velocity by factoring spatially variable filters, and
non-stationary deconvolution.
The helical boundary conditions allow the 2-D convolution matrix to be
inverted directly without the need for splitting approximations, with
a cost that scales linearly with the size of the model space. Using
this methodology, a whole range of implicit depth migrations may now be
feasible in 3-D. domain provides a tool for
depth migration with strong lateral variations in velocity.
Implicit formulations of depth extrapolation have several advantages
over explicit methods.
However, the simple 3-D extension of conventional 2-D wavefield
extrapolation by implicit finite-differencing requires the
inversion of a 2-D convolution matrix which is computationally
difficult.
In this paper, we solve the 45 wave equation
with helical boundary conditions on one of the spatial axes.
These boundary conditions reduce the 2-D convolution
into an equivalent 1-D filter operation. We then factor this 1-D
filter into causal and anti-causal parts using an extension of
Kolmogoroff's spectral factorization method, and invert the
convolution operator efficiently by 1-D recursive filtering.
We include lateral variations
in velocity by factoring spatially variable filters, and
non-stationary deconvolution.
The helical boundary conditions allow the 2-D convolution matrix to be
inverted directly without the need for splitting approximations, with
a cost that scales linearly with the size of the model space. Using
this methodology, a whole range of implicit depth migrations may now be
feasible in 3-D.
|
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)