




Next: Spectra factorization
Up: Theory
Previous: Theory
Let g(a)=s-f(a) be the function whose roots we seek to find, where f(a)
is an arbitrary function and s is a constant. If we find the roots of
g(a)=0, then we also have found the roots of f(a)=s. Newton's iteration for
g(a)=0 can be written as
g(at)=-g'(at)(at+1-at), or
|
s-f(at)=f'(at)(at+1-at)
|
(1) |
If we now consider f(a)=a2, then we can write (1) as:
which gives Newton's iterative procedure for finding square roots
| 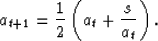 |
(3) |





Next: Spectra factorization
Up: Theory
Previous: Theory
Stanford Exploration Project
5/1/2000