




Next: The quadrature filter
Up: HILBERT TRANSFORM
Previous: HILBERT TRANSFORM
Let xt be an even function of t.
The definition 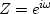 gives
gives
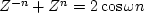 ; so
; so
| 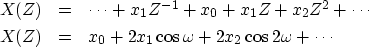 |
(1) |
| (2) |
Now make up a new function Y(Z)
by replacing cosine by sine in (2):
| 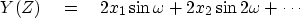 |
(3) |
Recalling that 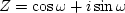 , we see
that all the negative powers of Z cancel from X(Z)+iY(Z), giving
a causal C(Z):
, we see
that all the negative powers of Z cancel from X(Z)+iY(Z), giving
a causal C(Z):
| ![\begin{displaymath}
C(Z) \eq
{1\over 2} [X(Z)+iY(Z)] \eq
{1\over 2} x_0 + x_1 Z + x_2 Z^2 + \cdots \ \end{displaymath}](img7.gif) |
(4) |
Thus, for plot pairs, the causal response is ct,
the real part of the FT is equation (2),
and the imaginary part not usually shown
is given by equation (3).





Next: The quadrature filter
Up: HILBERT TRANSFORM
Previous: HILBERT TRANSFORM
Stanford Exploration Project
10/21/1998