




Next: A BUTTERWORTH-FILTER COOKBOOK
Up: SPECTRAL FACTORIZATION
Previous: Pathological examples
As we learned from equation (19),
a minimum-phase function is determined completely from its spectrum.
Thus its phase is determinable from its spectrum.
Likewise, we will see that, except for a scale,
the spectrum is determinable from the phase.
So far we have not discussed the fact that
spectral factorization implicitly uses Hilbert transformation.
Somehow we simply generated a phase.
To see how the phase arose,
recall equation (18) and (19):
| 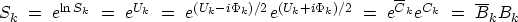 |
(20) |
Where did 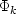 come from?
We took Uk + i 0 to the time domain, obtaining ut.
Then we multiplied ut by a real-valued step function of time.
This multiplication in the time domain
is what created the phase,
because multiplication in the time domain
implies a convolution
in the frequency domain.
Recall that the Fourier transform of a real-valued step function
arises with Hilbert transform.
Multiplying in time with a step means that,
in frequency, Uk has been convolved
with
come from?
We took Uk + i 0 to the time domain, obtaining ut.
Then we multiplied ut by a real-valued step function of time.
This multiplication in the time domain
is what created the phase,
because multiplication in the time domain
implies a convolution
in the frequency domain.
Recall that the Fourier transform of a real-valued step function
arises with Hilbert transform.
Multiplying in time with a step means that,
in frequency, Uk has been convolved
with 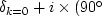 phase-shift filter).
So Uk is unchanged and a phase,
phase-shift filter).
So Uk is unchanged and a phase,  , has been generated.
This explanation will be somewhat clearer
if you review the Z-transform approach discussed
at the beginning of the chapter,
because there we can see both the frequency domain
and the time domain in one expression.
, has been generated.
This explanation will be somewhat clearer
if you review the Z-transform approach discussed
at the beginning of the chapter,
because there we can see both the frequency domain
and the time domain in one expression.
To illustrate different classes of discontinuity,
pulse, step, and slope,
Figure 13 shows another Hilbert-transform pair.
hilb2
Figure 13
A Hilbert-transform pair.

EXERCISES:
-
What is the meaning of minimum-phase waveform if the
roles of the time and frequency domains
are interchanged?
-
Show how to do the inverse Hilbert transform:
given
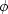 , find u.
What is the interpretation of the fact that we cannot get u0?
, find u.
What is the interpretation of the fact that we cannot get u0?
-
Consider a model of a portion of the earth where x is the north
coordinate, +z represents altitude above the earth,
and magnetic bodies are distributed in the earth, creating
no component of
magnetic field in the east-west direction.
We can show that the magnetic field h above the earth is represented by
![\begin{displaymath}
\left[
\begin{array}
{cc}
h_x (x, z) \ h_z (x, z) \end{arr...
...t k\vert \end{array} \right] \,
e^{ikx - \vert k\vert z} \, dk \end{displaymath}](img68.gif)
Here F(k) is some spatial frequency spectrum.
- (a)
- By using Fourier transforms,
how do you compute hx(x, 0) from
hz (x, 0) and vice versa?
- (b)
- Given hz(x, 0), how do you compute hz(x, z)?
- (c)
- Notice that, at z = 0,
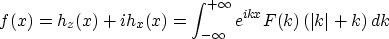
and that F(k) (|k| + k) is a one-sided function of k.
With a total field magnetometer we observe that
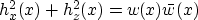
What can you say about obtaining F(k) from this?
- (d)
- How unique are hx(x) and hz(x) if
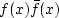 is given?
is given?
-
Test this idea:
write code to factor X(Z) into X(Z)=A(Z)B(Z),
where B(Z) is minimum-phase and A(Z) is maximum-phase.
Maximum-phase means that ZN A(1/Z) is minimum-phase.
First compute
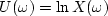 .Then remove a linear trend in the phase of
.Then remove a linear trend in the phase of 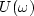 to get N.
Then split U
with its trend removed
into causal and anticausal parts
U(Z) = C-(1/Z) + C+(Z).
Finally, form
to get N.
Then split U
with its trend removed
into causal and anticausal parts
U(Z) = C-(1/Z) + C+(Z).
Finally, form
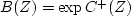 and
and
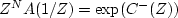 .
.





Next: A BUTTERWORTH-FILTER COOKBOOK
Up: SPECTRAL FACTORIZATION
Previous: Pathological examples
Stanford Exploration Project
10/21/1998

![]()
![]()
![]()