Next: Narrow-band data
Up: 2-D INTERPOLATION BEYOND ALIASING
Previous: The regression codes
Here we will see how to remove the small noise we are seeing in the
interpolated outputs.
The filter (10)
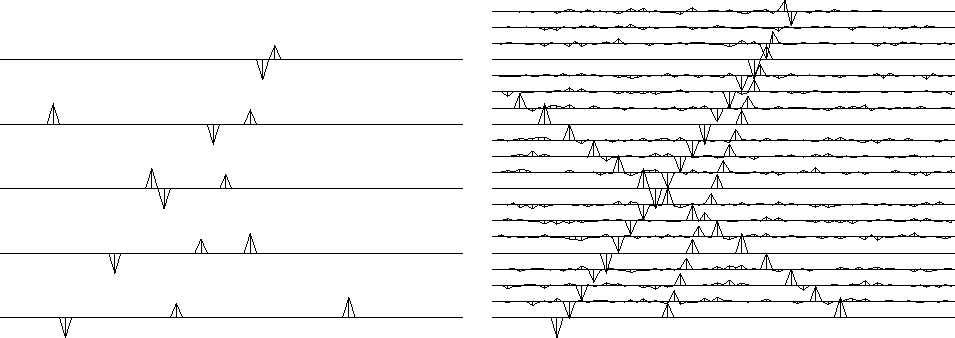
obviously destroys the input in Figure 14.
On the output interpolated data,
the filter-output residuals (not shown)
were all zeros despite the small noises.
The filter totally extinguishes the small noise on the outputs
because the noise has the same stepout (slope) as the signals.
The noise is absent from the original traces, which are interlaced.
How can dipping noises exist on the interpolated traces
but be absent from the interlaced data?
The reason is that one dip can interfere
with another to cancel on the known, noise-free traces.
The filter (10) destroys perfect output data
as well as the noisy data in Figure 14.
Thus, there is more than one solution to the problem.
This is the case in linear equation solving whenever
there is a null space.
Since we manufactured many more data points than we originally had,
we should not be surprised by the appearance of a null space.
When only a single dip is present,
the null space should vanish
because the dip vanishes on the known traces, having
no other dips to interfere with it there.
Confirm this by looking back at Figure 17,
which contains no null-space noise.
This is good news, because in real life,
in any small window of seismic data,
a single-dip model is often a good model.
If we are to eliminate the null-space noises,
we will need some criterion in addition to stepout.
One such criterion is amplitude:
the noise events are the small ones.
Before using a nonlinear method,
we should be sure, however, that
we have exploited the full power of linear methods.
Information in the data is carried by the envelope functions,
and these envelopes have not been included in the analysis so far.
The envelopes can be used to make weighting functions.
These weights are not weights on residuals, as
in the routine iner() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
These are weights on the solution.
The
.
These are weights on the solution.
The 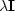 stabilization
in routine
pe2()
stabilization
in routine
pe2() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) applied uniform weights using
the subroutine
ident()
applied uniform weights using
the subroutine
ident() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
as has been explained.
Here we simply apply variable weights
,
as has been explained.
Here we simply apply variable weights 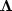 using
the subroutine diag()
using
the subroutine diag() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The weights themselves are the inverse of the envelope of input data
(or the output of a previous iteration).
Where the envelope is small lies a familiar problem, which
I approached in a familiar way--by adding a small constant.
The result is shown in Figure 19.
.
The weights themselves are the inverse of the envelope of input data
(or the output of a previous iteration).
Where the envelope is small lies a familiar problem, which
I approached in a familiar way--by adding a small constant.
The result is shown in Figure 19.
wlace3
Figure 19
Top left is input.
Top right is the interpolation with uniform weights.
In the middle row are
the envelope based on input data
and the corresponding interpolated data.
For the bottom row, the middle-row solution was used
to design weights from which a near-perfect solution
was derived.





The top row is the same as Figure 13.
The middle row shows the improvement that can be expected
from weighting functions based on the inputs.
So the middle row is the solution to a linear interpolation problem.
Examining the envelope function on the middle left,
we can see that it is a poor approximation
to the envelope of the output data,
but that is to be expected because
it was estimated by smoothing the absolute values
of the input data (with zeros on the unknown traces).
The bottom row is a second stage of the process just described,
where the new weighting function is based on the result
in the middle row.
Thus the bottom row is a nonlinear operation on the data.
When interpolating data, the number of unknowns is large.
Here each row of data is 75 points,
and there are 20 rows of missing data.
So, theoretically, 1500 iterations might be required.
I was getting good results with 15 conjugate-gradient iterations
until I introduced weighting functions;
then the required number of iterations jumped to about a hundred.
The calculation takes seconds
(unless the silly computer starts to underflow;
then it takes me 20 times longer.)
I believe the size of the dynamic range in the weighting function
has a controlling influence on the number of iterations.
Before I made
Figure 19,
I got effectively the same result, and more quickly,
using another method, which I abandoned because its philosophical
foundation was crude.
I describe this other method here only
to keep alive the prospect of exploring the issue of the speed
of convergence.
First I moved the ``do iter'' line above the already indented
lines to allow for the nonlinearity of the method.
After running some iterations with 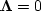 to ensure the emergence of some big interpolated values,
I turned on
to ensure the emergence of some big interpolated values,
I turned on 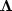 at values below a threshold.
In the problem at hand, convergence speed is not important economically
but is of interest because we have so little guidance as to
how we can alter problem formulation in general
to increase the speed of convergence.
at values below a threshold.
In the problem at hand, convergence speed is not important economically
but is of interest because we have so little guidance as to
how we can alter problem formulation in general
to increase the speed of convergence.





Next: Narrow-band data
Up: 2-D INTERPOLATION BEYOND ALIASING
Previous: The regression codes
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
These are weights on the solution.
The
.
These are weights on the solution.
The ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) applied uniform weights using
the subroutine
ident()
applied uniform weights using
the subroutine
ident() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
as has been explained.
Here we simply apply variable weights
,
as has been explained.
Here we simply apply variable weights ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The weights themselves are the inverse of the envelope of input data
(or the output of a previous iteration).
Where the envelope is small lies a familiar problem, which
I approached in a familiar way--by adding a small constant.
The result is shown in Figure 19.
.
The weights themselves are the inverse of the envelope of input data
(or the output of a previous iteration).
Where the envelope is small lies a familiar problem, which
I approached in a familiar way--by adding a small constant.
The result is shown in Figure 19.